Bài 1, 2 trang 101 SBT Toán 7 tập 2

Bài 1, 2 trang 101 SBT Toán 7 tập 2

Bài 1: Cho hình 107 trong đó ∠B = 40°, ∠D = 130°, AB // DE. Tính ∠BCD.

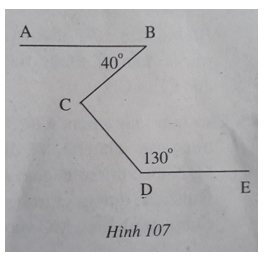
Lời giải:

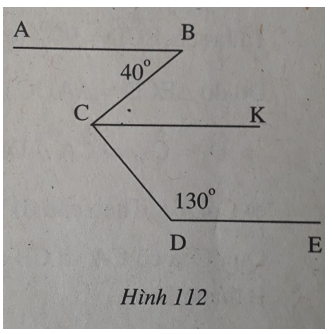
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.

AB // CK ⇒ ∠BCK = ∠B = 40° (so le trong)

CK // DE ⇒ ∠DCK bù ∠CDE (góc trong cùng phía)

⇒ ∠DCK = 180° - 130° = 50°.

Do đó: ∠BCD = ∠BCK + ∠DCK = 40° + 50° = 90°.

Bài 2: Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng:

a) CE = OD;    b) CE ⊥ CD;

c) CA = CB;    d) CA // DE;

e) Ba điểm A, B, C thẳng hàng.

Lời giải:

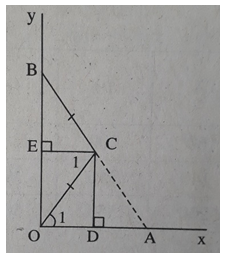
a) CE // OD (cùng vuông góc với OB) ⇒ ∠C₁ = ∠O₁ (so le trong)

ΔOCE = ΔCOD (cạnh huyền – góc nhọn) ⇒ CE = OD.

b) CD // OE (cùng vuông góc OA) ⇒ ∠(BEC) = ∠(ECD) (so le trong)

Ta lại có ∠(BEC) = 90° nên ∠(ECD) = 90°.

Vậy CE ⊥ CD.

c) CD là đường trung trực của OA ⇒ CO = CA.

CE là đường trung trực của OB ⇒ CO = CB.

Do đó CA = CB.

d) (h.114) Ta có CE = OD (câu a))

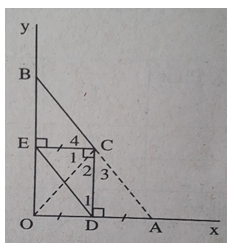
mà OD = DA nên CE = DA.

Ta lại có ∠(ECD) = 90° (câu b)).

Do đó ΔECD = ΔADC (c.g.c)

⇒ ∠D₁ = ∠C₃ ⇒ CA // DE (hai góc so le trong bằng nhau).

e) Cách 1: Theo câu d): CA // DE. Chứng minh tương tự: CB // DE.

Qua C ta có CA và CB cùng song song với DE nên theo tiên đề Ơ-clit: A, C, B thẳng hàng.

Cách 2: CO = CA ⇒ ΔOCA cân ⇒ đường cao CD là đường phân giác của góc OCA ⇒ ∠C₂ = ∠C₃ ⇒ ∠(OCA) = 2∠C₂ .

Chứng minh tương tự: ∠C₁ = ∠C₄ ⇒ ∠(OCB) = 2∠C₁.

Do đó:

∠(OCA) + ∠(OCB) = 2∠C₂ + 2∠C₁ = 2(∠C₂ + ∠C₁) = 2∠(ECD) = 2.90° = 180°.

Vậy A, C, B thẳng hàng.