Bài 3, 4, 5, 6, 7, 8, 9 trang 102 SBT Toán 7 tập 2

Bài 3, 4, 5, 6, 7, 8, 9 trang 102 SBT Toán 7 tập 2

Bài 3: Tìm giá trị của x trên hình 108 biết rằng AB // DE

Lời giải:

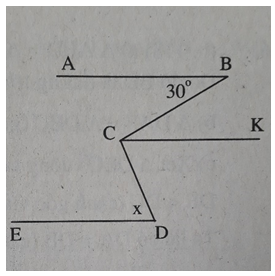
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.

Ta có AB // CK ⇒ ∠(BCK) = ∠B = 30° (so le trong)

Suy ra

∠(DCK) = ∠(BCD) - ∠(BCK) = 100° - 30° = 70°.

CK // DE ⇒ ∠D = ∠(DCK) = 70° (so le trong)

Vậy x = 70°.

Bài 4: So sánh các cạnh của tam giác CDE trên hình 109 biết rằng BE // CD.

Lời giải:

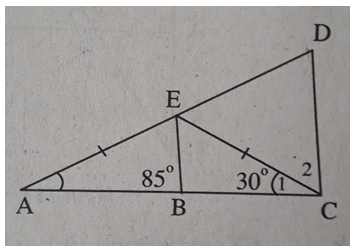
Trước hết ta tính các góc của ΔECD.

ΔAEC cân tại E ⇒ ∠A = ∠C₁ = 30°.

∠(CED) là góc ngoài của ΔAEC.

⇒ ∠(CED) = A + ∠C₁ = 30° + 30° = 60°.

BE // CD ⇒ ∠(ACD) = ∠(ABE) = 85° (đồng vị)

⇒ ∠C₂ = ∠(ACD) - ∠C₁ = 85° - 30° = 55°.

Xét ΔECD: ∠D = 180° - ∠(CED) - ∠C₂ = 180° - 60° - 55° = 65°.

Trong ΔECD: ∠C₂ < ∠(CED) < ∠D ⇒ ED < CD < EC.

Bài 5: Cho tam giác ABC vuông góc tại A, phân giác BD.

a) So sánh các độ dài AB và AD;

b) So sánh các độ dài BC và BD.

Lời giải:

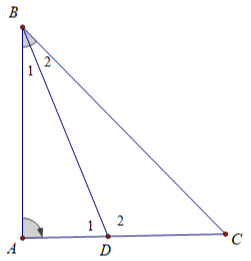
a) ∠D₁ > ∠B₂ (góc ngoài của ΔBDC)

Mà ∠B₁ = ∠B₂ nên ∠D₁ > ∠B₁ .

ΔABD có ∠D₁ > ∠B₁ nên AB > AD.

b) Cách 1. ∠D₂ > ∠A (góc ngoài của ΔABD)

mà ∠A = 90° nên ∠D₂ > 90°.

ΔBDC có ∠D₂ > 90° nên ∠D₂ > ∠C , do đó BC > BD.

Cách 2. Xét các đường xiên BD, BC. Hình chiếu AC > AD nên đường xiên BC > BD.

Bài 6: Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng:

a) BD là đường thẳng trung trực của AE;

b) DF = DC;

c) AD > DC.

Lời giải:

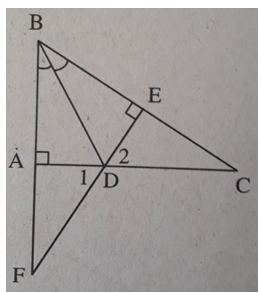
a) ΔABD = ΔEBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.

Do đó BD là đường trung trực của AE.

b) ΔDEF = ΔDEC (g.c.g) ⇒ DF = DC.

c) Xét ΔDEC vuông tại E:

DE < DC (cạnh góc vuông nhỏ hơn cạnh huyền)

Ta lại có DA = DE (câu a)) nên DA < DC.

Bài 7: a) Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC thì tam giác đo vuông tại A.

b) Ứng dụng: Một tờ giấy bị rách ở mép (h.110). Hãy dùng thước và compa vẽ đường vuông góc với AB tại A.

Hướng dẫn: Vẽ điểm C sao cho CA = CB, rồi vẽ điểm E thuộc tia đối của tia CB sao cho CE = CB.

Lời giải:

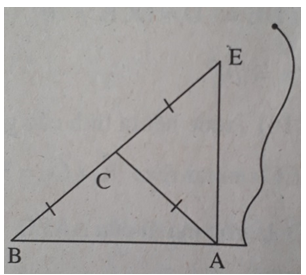
a) Xem chứng minh ở bài 39.

b) (h.119) ΔABE có đường trung tuyến AC bằng 1/2 BE nên ∠(BAE) = 90°.

Vậy AE ⊥ AB.

Bài 8: Cho tam giác ABC, đường cao AH. Vẽ điểm D sao cho AB là đường trung trực của HD. Vẽ điểm E sao cho AC là đường trung trực của HE. Gọi M, N theo thứ tự là giao điểm của DE với AB, AC. Xét xem các đường thẳng sau là các đường gì trong tam giác HMN: MB, NC, HA, HC, MC, từ đó hãy chứng minh rằng MC vuông góc với AB.

Lời giải:

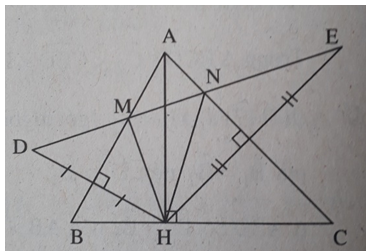
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của ΔHMN.

Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác của góc trong của ΔHMN.

HC vuông góc với HA tại H nên HC là đường phân giác góc ngoài của ΔHMN.

Các đường thẳng HC và NC cắt nhau tại C nên MC là đường phân giác góc trong của ΔHMN.

MB và MC là các tia phân giác của hai góc kề bù nên MB ⊥ MC.

Vậy MC ⊥ AB.

Bài 9: Tam giác ABC vuông tại A, đường cao AH, HC – HB = AB. Chứng minh rằng BC = 2AB.

Lời giải:

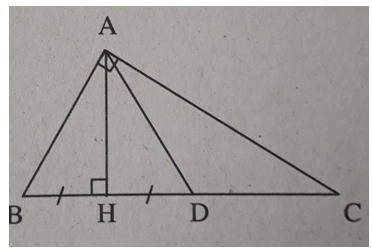
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao là trung tuyến nên là tam giác cân, suy ra

∠(ADB) = ∠B .    (1)

Ta có: DC = HC – HD = HC – HB = AB = AD

Nên ΔADC cân, do đó ∠(DAC) = ∠C , suy ra

∠(DAB) = ∠B .    (2)

Từ (1) và (2) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.

Suy ra AB = BD = AD = DC. Vậy BC = 2AB.