Bài 36, 37, 38, 39, 40, 41, 42, 43 trang 142 SBT Toán 7 tập 1
Bài 36, 37, 38, 39, 40, 41, 42, 43 trang 142 SBT Toán 7 tập 1
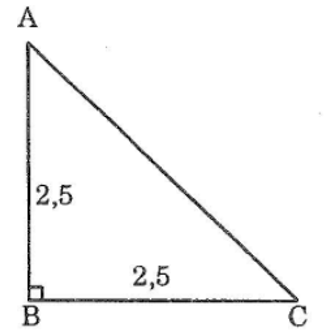
Bài 36: Vẽ tam giác ABC biết BA = BC = 2,5 cm; ∠B = 90°. Sau đó đo các góc A và C để kiểm tra rằng ∠A = ∠C = 45°
Lời giải:
Ta có: BA = BC = 2,5 cm
Suy ra : ΔABC cân tại B
Vậy: ∠A = ∠C = (180-∠B )/2 = (180 - 90)/2 = 45°
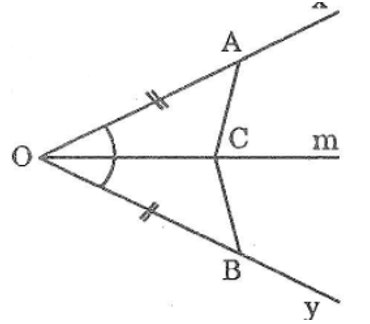
Bài 37: Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOC = ΔBOC theo trường hợp cạnh-góc-cạnh.
Lời giải:
Cho góc nhọn xOy. Trên tia Ox lấy điểm A trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm C trên tia Om của góc xOy. Chứng minh rằng ΔAOC = ΔBOC
Bài 38: Qua trung điểm I của đoạn thẳng AB, kẻ đường vuông góc với AB, trên đường vuông góc đó lấy hai điểm C và D. nối CA, CB, DA, DB.
Tìm các cặp tam giác bằng nhau trong hình vẽ.
Lời giải:
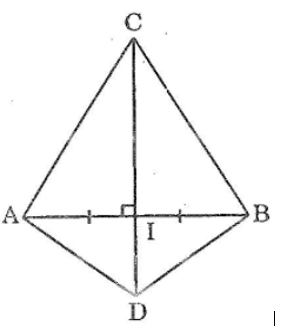
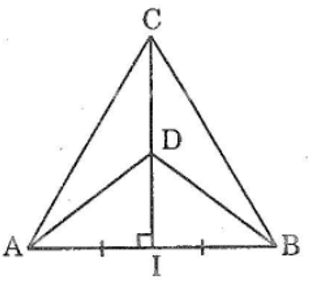
ta có: ΔAIC = ΔBIC(c.g.c)
ΔAID = ΔBID(c.g.c)
ΔACD = ΔBCD(c.c.c)
Bài 39: Vẽ ΔABC có ∠A = 90°, AB = 3cm, AC = 1cm. Sau đó đo góc C để kiểm tra rằng ∠C ≈ 72°.
Lời giải:
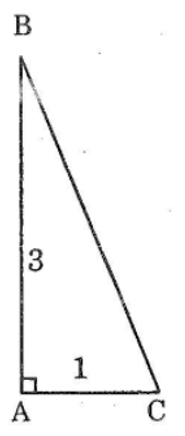
Ta có: ΔABC có ∠A = 90°, AB = 3cm, AC = 1cm
Suy ra: ∠C ≈ 72°.
Bài 40: Qua trung điểm M của đoạn AB, kẻ đường thẳng vuông góc với AB lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB
Lời giải:
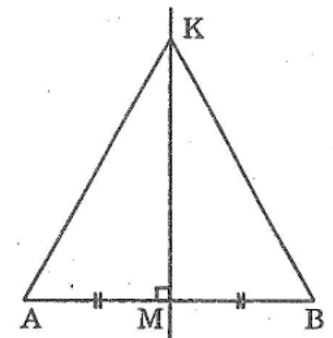
Xét ΔAMK và ΔBMK, ta có:
AM = BM (gt)
∠(AMK) = ∠(BMK) = 90° (vì KM ⊥ AB)
Mk cạnh chung
Suy ra: ΔAMK = ΔBMK(c.g.c)
⇒ ∠(AKM) = ∠(BKM)
Vậy KM là tia phân giác của góc AKB
Bài 41: Hai đoạn thẳng AB và CD căt nhau tại trung điểm O của mối đoạn. Chứng minh rằng AC // BD
Lời giải:
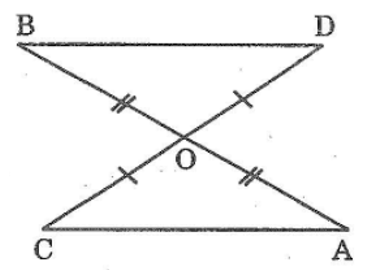
Xét Δ AOC và Δ BOD, ta có:
OA = OB (gt)
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒ ∠A = ∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Bài 42: Cho tam giác ABC có ∠A = 90°. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE
Lời giải:
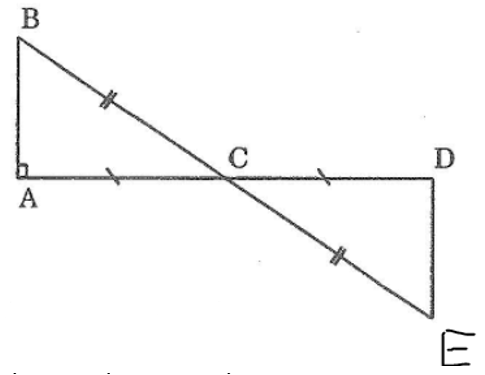
Xét ΔABC và ΔDEC, ta có:
AC = DC (gt)
∠(ACB) = ∠(ECD) (đối đỉnh)
BC = EC (gt)
Suy ra: ΔABC = ΔDEC (c.g.c)
⇒ ∠A = ∠D (hai góc tương ứng).Mà ∠A = 90° nên ∠D = 90°
Bài 43: Cho tam giác ABC có ∠A = 90°, trên cạnh BC lấy điểm E sao cho BE = BA. Trên tia phân giác của góc B cắt AC ở D
a, So sánh các độ dài DA và DE
b, Tính số đo góc BED
Lời giải:
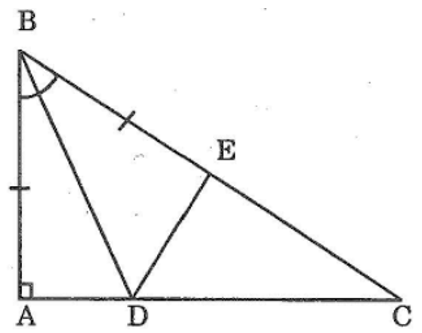
a, Xét ΔABD và ΔEBD, ta có:
AB = BE (gt)
∠(ABD) = ∠(DBE) (vì Bd là tia phân giác)
BC cạnh chung
Suy ra: ΔABD và ΔEBD(c.g.c)
⇒ DA = DE (hai cạnh tương ứng)
b, Ta có: ΔABD và ΔEBD(chứng minh trên)
Suy ra: ∠A = ∠(BED) (hai góc tương ứng)
Mà ∠A = 90° nên ∠(BED) = 90°

