Bài 44, 45, 46, 47, 48 trang 143 SBT Toán 7 tập 1

Bài 44, 45, 46, 47, 48 trang 143 SBT Toán 7 tập 1

Bài 44: Cho tam giác AOB có OA = OB. Tia phân giác của góc O cắt AB ở D. chứng minh rằng:

a. Giải DA = DB

b. OD ⊥ AB

Lời giải:

a, Xét ΔAOD và ΔBOD, ta có:

OA = OB (gt)

∠(AOD) = ∠(BOD)(vì OD là tia phân giác)

OD cạnh chung

Suy ra: ΔAOD = ΔBOD(c.g.c)

Vậy: DA = DB (hai cạnh tương ứng)

b, ΔAOD = ΔBOD (chứng minh trên)

⇒ ∠(D₁ ) = ∠(D₂ ) (hai góc tương ứng)

Ta có: ∠(D₁ ) + ∠(D₂ ) = 180° (hai góc kề bù)

Suy ra: ∠(D₁ ) = ∠(D₂ ) = 90°

Vậy: OD ⊥ AB

Bài 45: Cho các đoạn thẳng AB và CD trên giấy kẻ ô vuông (hình dưới ). Chứng minh rằng AB = CD, AB // CD

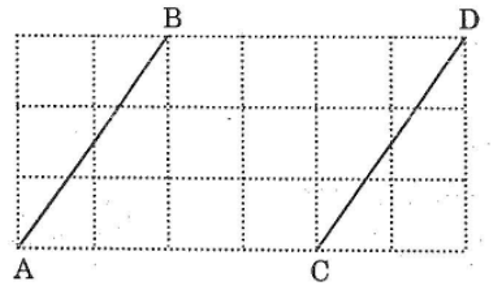
Lời giải:

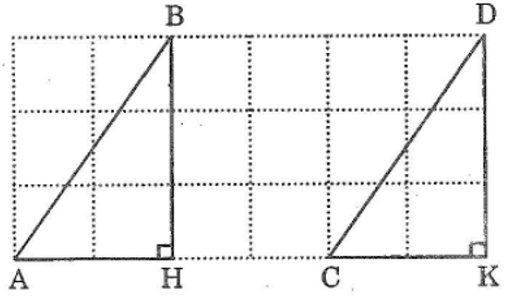
Gọi giao điểm của đường kẻ ô vuông đi qua điểm A và đi qua điểm B cắt nhau tại H; đi qua điểm C và đi qua điểm D là K.

Xét ΔAHB và ΔCKD, ta có:

AH = CK (gt)

∠(AHB) = ∠(CKD) =90o

BH = DK (bằng 3 ô vuông)

Suy ra ΔAHB = ΔCKD (c.g.c)

⇒ AB = CD và ∠(BAH) = ∠(DCK)

Hai đường thẳng AB Và CD cắt đường thẳng AK có 2 góc ∠(BAH) và ∠(DCK) ở vị trí đồng vị bằng nhau nên AB // CD.

Bài 46: Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng:

a. BC = BE

b. DC ⊥ BE

Lời giải:

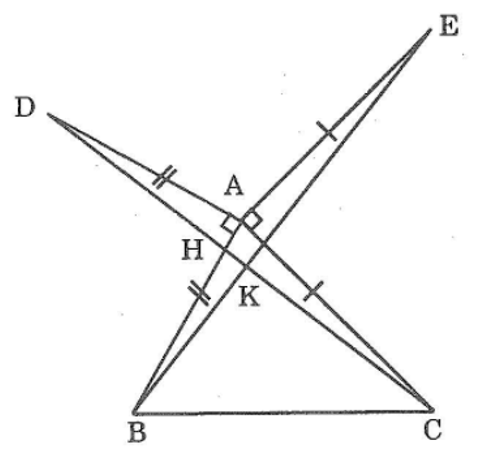
a, Xét ΔABE và ΔACD, ta có:

AB = AD (gt)

AE = AC (gt)

∠(BAE) = ∠(BAC) + 90°

suy ra: (BAE) = (CAD)

⇒ ΔABE = ΔADC (c.g.c)

⇒ DE = BE (2 cạnh tương ứng)

b, Gọi giao điểm DC và AB là H, giao điểm của Cd và BE là K

Ta có: ∠(ABE) = ∠D     (1)

Trong tam giác vuông AHD, ta có: (HAD) =90o

⇒ ∠D +∠(AHD) = 90° (tính chất tam giác vuông)     (2)

Mà ∠(AHD) = ∠(KHB)(đối đỉnh)     (3)

Từ (1), (2) và (3) suy ra:

∠(ABE) +∠(KHB) = 90°

Trong Δ KHB ta có:

∠(KHB) +∠(ABE) + ∠(BKH) = 180° (tổng 3 góc trong tam giác)

⇒ ∠(BKH) = 180° - ((∠ABE) + (∠BKH)) = 180° - 90° = 90°

Vậy DC ⊥ BE

Bài 47: Cho tam giác ABC có ∠B = 2∠C . Tia phân giác của góc B cắt AC ở D. trên tia đối của tia BD lấy điểm E sao cho BE = AC. Trên tia đối của tia CB lấy điểm K sao cho CK = AB. Chứng minh rằng AE = AK.

Lời giải:

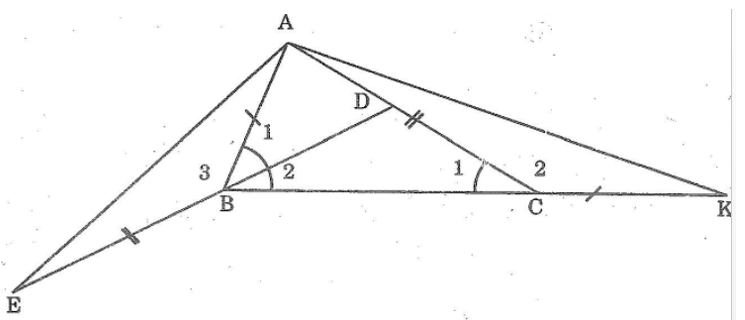
Ta có: ∠B = 2∠(C₁ ) (gt) ⇒ ∠(C₁ ) = (1/2 )∠B

Lại có: ∠(B₁ ) + ∠(B₂ ) (vì BD là tia phân giác) ⇒ ∠(C₁ ) = ∠(B₁ )     (1)

∠(C₁ ) + ∠(C₂ ) = 180° (kề bù)     (2)

∠(B₁ ) + ∠(B₃ ) = 180° (kề bù)     (3)

Từ (1), (2) và (3) suy ra: ∠(C₂ ) = ∠(B₃ )

Xét ΔABE và ΔACK, ta có:

AB = KC (gt)

∠(B₃ ) = ∠(C₂ ) (chứng minh trên)

BE = CA (gt)

Suy ra : ΔABE = ΔACK (c.g.c)

Vậy :AE = AK(hai cạnh tương ứng)

Bài 48: Cho tam giác ABC, K là trung điểm của AB, E là trung điểm của AC. Trên tia đối của tia KC lấy điểm M sao cho KM = KC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng A là trung điểm của MN

Lời giải:

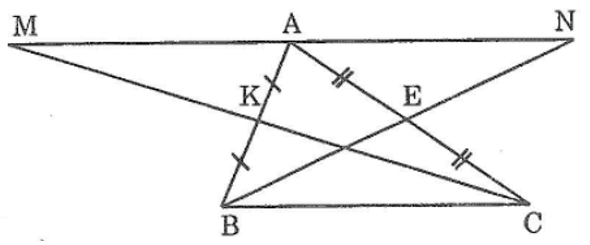
Xét ΔAKM và ΔBKC ta có:

AK = BK (gt)

∠(AKM) = ∠(BKC) (đối đỉnh)

KM = KC

Suy ra: ΔAKM v= ΔBKC(c.g.c)

⇒ AM = BC (hai cạnh tương ứng)

∠(AMK) = ∠(BCK) (2 góc tương ứng)

Suy ra: Am // BC ( vì có cặp góc so le trong bằng nhau)

Tương tự: ΔAEN = ΔCEB(c.g.c)

⇒ AN = BC (2 cạnh tương ứng)

∠(EAN) = ∠(ECB) (2 góc tương ứng)

Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)

Ta có: Am // BC và AN // BC nên hai đường tahwngr Am và AN trùng nhau hay A,M,N thẳng hàng     (1)

AM = AN ( vì cùng bằng BC)     (2)

Từ (1) và (2) suy ra: A là trung điểm của MN