Bài 4.4 trang 144 SBT Toán 7 tập 1

Bài 4.4 trang 144 SBT Toán 7 tập 1

Bài 4.4: Cho tam giác ABC có ∠A = 110°, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA.

a) Tính số đo của góc ACK.

b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD = AB, AE vuông góc với AC và AE = AC. Chứng minh rằng ΔCAK = ΔAED

c) Chứng minh rằng MA vuông góc với DE.

Lời giải:

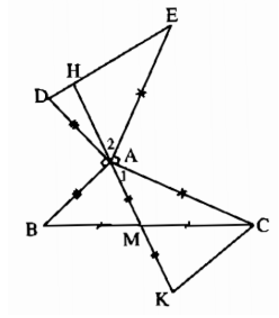
a) Chứng minh CK // AB để suy ra

∠ACK = 180° - ∠BAC = 180° - 110° = 70°.

b) ΔCAK = ΔAED (c.g.c)

c) Gọi H là giao điểm của MA và DE.

ΔCAK = ΔAED nên ∠A₁ = ∠E.

Ta lại có ∠A₁ + ∠A₂ = 90° nên ∠A₂ + ∠E = 90°.

Do đó MA ⊥ DE.