Bài 40, 41 trang 44 SBT Toán 7 tập 2

Bài 40, 41 trang 44 SBT Toán 7 tập 2

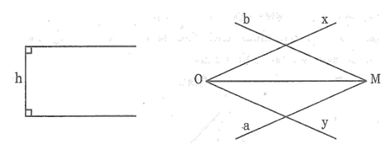
Bài 40: Hình sau là thước có khoảng cách giữa hai lề song song với nhau bằng h. Để vẽ tia phân giác của góc xOy, ta áp một lề của thước vào cạnh Oy ta kẻ được đường thẳng b. Vì sao giao điểm M của a và b nằm trên tia phân giác của góc xOy?

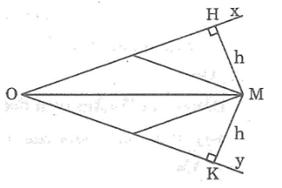
Lời giải:

Kẻ MH ⊥ Ox, MK ⊥ Oy.

Khi đó:

MH là chiều rộng của thước hai lề

MK là chiều rộng của thước hai lề

Mà chiều rộng của thước đó bằng nhau và bằng h nên ta có:

MH = MK = h

Điểm M nằm trong góc xOy và cách đều hai cạnh của góc nên M thuộc tia phân giác của góc xOy.

Bài 41: Cho tam giác ABC. Chứng minh rằng hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.

Lời giải:

Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.

Kẻ KE ⊥ BC, KF ⊥ AC, KD ⊥ AB

Vì K nằm trên phân giác của ∠(CBD) nên:

KD = KE (tính chất tia phân giác)    (1)

Vì K nằm trên tia phân giác của ∠(BCF) nên:

KE KF (tính chất tia phân giác)    (2)

Từ (1) và (2) suy ra: KD = KF

Điểm K nằm trong ∠(BAC) cách đều 2 cạnh AB và AC nên K nằm trên tia phân giác của ∠(BAC) .