Bài 49, 50, 51, 52, 53, 54 trang 144 SBT Toán 7 tập 1

Bài 49, 50, 51, 52, 53, 54 trang 144 SBT Toán 7 tập 1

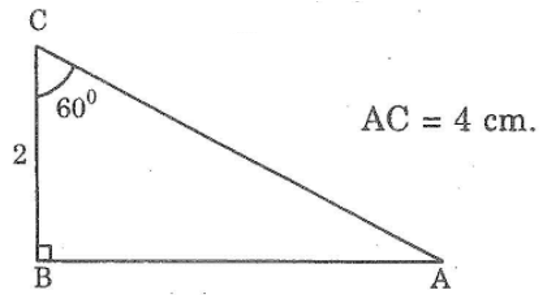
Bài 49: Vẽ tam giác ABC biết ∠B = 90°, ∠C = 60°, BC = 2cm. Sau đó đo AC để kiểm tra rằng AC = 4cm.

Lời giải:

Bài 50: Tìm các tam giác bằng nhau ở hình dưới (không xet tam giác mà các cạnh chưa được kẻ)

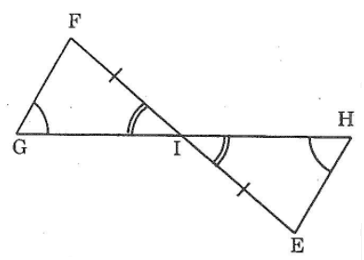
Lời giải:

Ta có: ΔABD = ΔCBD (g.c.g)

ΔGIF = ΔHIE (g.c.g)

Bài 51: Cho tam giác ADE có ∠AD = ∠AE . Tia phân giác của góc D cắt AE ở điểm M. tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dịa DN và EM

Lời giải:

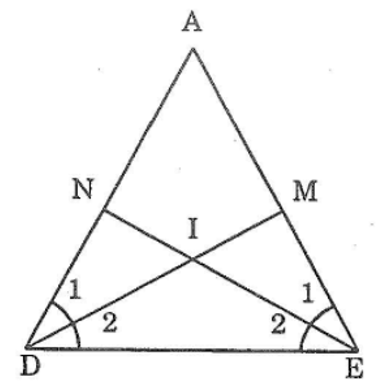
Tam giác ADE có: ∠D = ∠E (gt)

∠(D₁ ) = ∠(D₂ ) = (1/2)∠D (vì DM là tai phân giác)

∠(E₁ ) = ∠(E₂ ) = (1/2)∠E (vì EN là tia phân giác)

Suy ra: ∠(D₁ ) = ∠(D₂ ) = ∠(E₁ ) = ∠(E₂ )

xét ΔDNE và ΔEMD, ta có:

∠(NDE) = ∠(MED) (gt)

DE cạnh chung

∠(D₂ ) = ∠(E₂ ) (chứng minh trên)

Suy ra: ΔDNE = ΔEMD (g.c.g)

Vậy DE = EM (hai góc tương ứng)

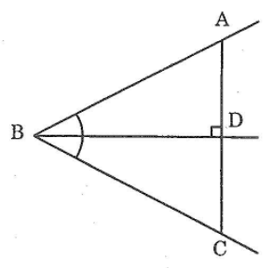
Bài 52: Cho hình bên, trong dod AB // HK, AH // BK.Chứng minh rằng AB = HK; AH = BK

Lời giải:

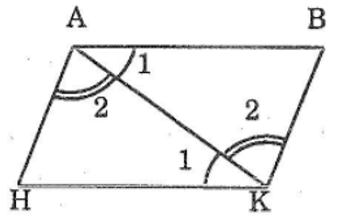
Nối AK, ta có:

AB // HK (gt)

⇒ ∠(A₁ ) = ∠(K₁ ) (hai góc so le trong)

AH // BK (gt)

⇒ ∠ (A₂ ) = -∠(K₂ ) (hai góc so le trong)

Xét ΔABK và ΔKHA, ta có:

∠(A₁ ) = ∠(K₁ )

AK canh chung

∠(A₂ ) = ∠(K₂ )

Suy ra: ΔABK = ΔKHA (g.c.g)

Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)

Bài 53: Cho tam giác ABC. Các tua phân giác của các góc B và C cắt nhau ở O. Kẻ OD ⊥ AC, kẻ OE ⊥ AB. Chứng minh rằng OD = OE

Lời giải:

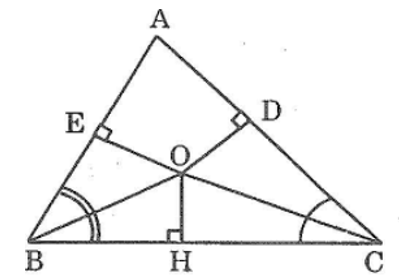
Kẻ OH ⊥ BC

Xét hai tam giác vuông OEB và OHB, ta có:

∠(OEB) = ∠OHB = 90°

Cạnh huyền OB chung

∠(EBO) = ∠(HBO)

Suy ra Δ OEB = Δ OHB (cạnh huyền góc nhọn)

⇒ OE = OH (hai cạnh tương ứng)

Xét hai tam giác vuông OHC và ODC, ta có:

∠(OHC) = ∠ODC = 90°

Cạnh huyền OB chung

∠(HCO) = ∠(DCO)

Suy ra Δ OHC = Δ ODC (cạnh huyền góc nhọn)

⇒ OD = OH (hai cạnh tương ứng)

Từ (1) và (2) suy ra: OE = OD

Bài 54: Cho tam giác ABC có AB = AC. Lấy điểm D trân cạnh AB, điểm E trên cạnh AC sao cho AD = AE

a, Chứng minh rằng BE = CD

b, Gọi O là giao điểm của BE và CD

Chứng minh rằng ΔBOD = COE

Lời giải:

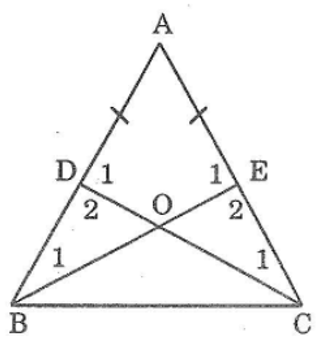
a. Xét ΔBEA và CDA, ta có:

BA = CA (gt)

∠A chung

AE = AD

Suy ra: ΔBEA = CDA (c.g.c)

Vậy: BE = CD (hai cạnh tương ứng)

b. ΔBEA = ΔCDA (chứng minh trên)

⇒ ∠(B₁ ) = ∠(C₁ ) ;∠(E₁ ) = ∠(D₁ ) (hai góc tương ứng)

∠(E₁ ) + ∠(E₂ ) = 180° (hai góc kề bù)

∠(D₁ ) + ∠(D₂ ) = 180° (hai góc kề bù)

Suy ra: ∠(E₂ ) = ∠(D₂ )

AB = AC (gt)

⇒ AE + EC = AD = BD MÀ AE = AD (GT) ⇒ EC = BD

Xét ΔODB và ΔOCE, ta có:

∠(E₂ ) = ∠(D₂ ) (chứng minh trên)

DB = EC (chứng minh trên)

∠(B₁ ) = ∠(C₁ )

Suy ra: ΔODB = ΔOCE