Bài 63, 64, 65, 66 trang 146 SBT Toán 7 tập 1

Bài 63, 64, 65, 66 trang 146 SBT Toán 7 tập 1

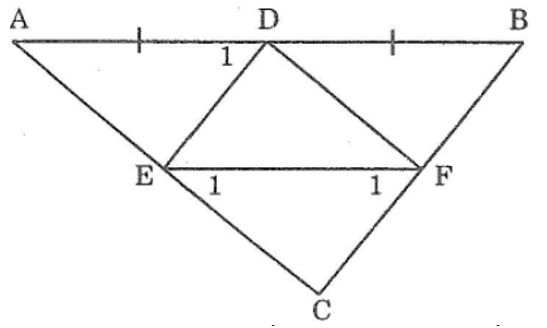
Bài 63: Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:

a. AD = EF

b. ΔADE = Δ EFC

c. AE = EC

Lời giải:

a, Xét Δ DBFvà Δ FDE, ta có:

∠(BDF) = ∠(DFE) (so le trong vì EF // AB)

DF cạnh chung

∠(DFB) = ∠(FDE) (so le trong vì DE // BC)

Suy ra: Δ DBF = Δ FDE(g.c.g) ⇒ DB = EF (hai cạnh tương ứng)

Mà AD = DB (gt)

Vậy: AD = EF

b, Ta có: DE // BC (gt)

⇒ ∠(D₁ ) = ∠B (đồng vị)

EF // AB (gt)

⇒ ∠(F₁ ) = ∠B (đồng vị)

⇒ ∠(E₁ ) = ∠A (đồng vị)

Xét Δ ADEvà Δ EFC, ta có:

∠(E₁ ) = ∠A (chứng minh trên)

AD = EF

∠(F₁ ) = ∠(D₁ ) (vì cùng bằng B)

Suy ra : Δ ADE = Δ EFC(g.c.g)

c,Vì : Δ ADE = Δ EFC nên AE = EC (hai cạnh tương ứng)

Bài 64: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng:

a, DB = CF

b, Δ BDC = Δ FCD

c, DE // BC và DE = 1/2BC

Lời giải:

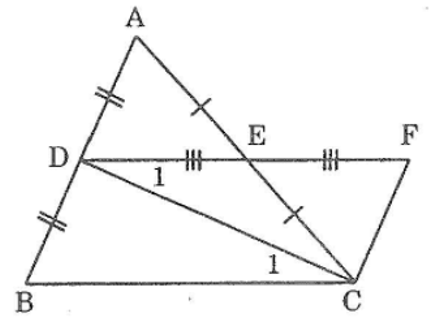
a, Xét ΔADE và ΔCFE, ta có:

AE = CE (gt)

∠(AED) = ∠(CEF) (đối đỉnh)

DE = FE

Suy ra: ΔADE = ΔCFE (c.g.c)

⇒ AD = CF (hai cạnh tương ứng)

Mà AD = DB (gt)

Vậy: DB = CF

b, Ta có: ΔADE = ΔCFE (chứng minh trên)

⇒ ∠(ADE) = ∠(CFE) (hai góc tương ứng)

Suy ra: AD // CF (vì có cặp góc so le trong bằng nhau)

Hay AB // CF

Xét ΔBDC và ΔFCD, ta có:

BD = CF (chứng minh trên)

∠(BDC) = ∠(FCD) (hai góc so le trong vì CF // AB)

DC cạnh chung

Suy ra: ΔBDC = ΔFCD (c.g.c)

c, Ta có: ΔBDC = ΔFCD (chứng minh trên)

Suy ra: ∠(C₁ ) = ∠(D₁ ) (hai góc tương ứng)

Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)

ΔBDC = ΔFCD suy ra BC = DF (hai cạnh tương ứng)

Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC

Bài 65: Cho tam giác ABC. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D và E, vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh rằng DM + EN = NC

Hướng dẫn: qua N kẻ đường thẳng song song với AB

Lời giải:

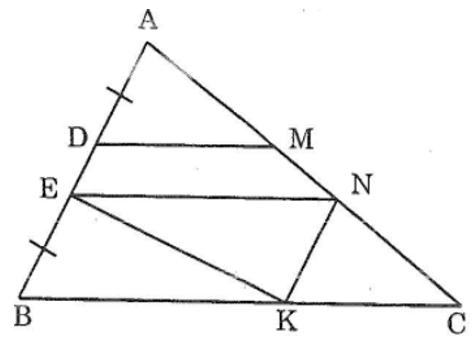
Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.

Xét ΔBEK và Δ NKE, ta có:

∠(EKB) = ∠(KEN) (so le trong vì EN // BC)

EK cạnh chung

∠(BEK) = ∠(NKE) (so le trong vì EN // BC)

Suy ra: Δ BEK = Δ NKE(g.c.g)

Suy ra: BE = NK (hai cạnh tương ứng)

EN = BK (hai cạnh tương ứng)

Xét Δ ADM và Δ NKC, ta có:

∠A = ∠(KNC) (đồng vị vì NK // AB)

AD = NK ( vì cùng bằng BE)

∠(ADM) = ∠(NKC) (vì cùng bằng góc B)

Suy ra: Δ ADM = Δ NKC(g.c.g)

Suy ra: DM = KC (hai cạnh tương ứng)

Mà BC = BK + KC. Suy ra: BC = EN + DM

Bài 66: Cho tam giác ABC có:∠ A = 60°

Các tia phân giác của các góc B, C cắt nhau ở I và cắt AC, AB theo thứ tự tại D, E. Chứng minh rằng: ID = IE

Hướng dẫn: kẻ tia phân giác góc BIC

Lời giải:

Trong ΔABC, ta có:

∠A + ∠B + ∠C = 180° (tổng ba góc trong tam giác)

⇒ ∠B + ∠C = 180 - ∠A = 180 - 60 = 120°

∠(B₁ ) = ∠(B₂ ) = 1/2 ∠B (gt)

∠(C₁ ) = ∠(C₂ ) = 1/2∠ C (gt)

Trong ΔBIC, ta có:

∠(BIC) = 180°(∠(B₁ ) + ∠(C₁ ) ) = 180° - (∠B /2+∠C /2) = 180° - 60° = 120°

Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K

Suy ra: ∠(I₂ ) = ∠(I₃ ) = 1/2 ∠(BIC) = 60°

Ta có: ∠(I₁ ) + ∠(BIC) = 180° (hai góc kề bù)

⇒ ∠(I₁ ) = 180° - ∠(BIC) = 180° - 120° = 60°

∠(I₄ ) = ∠(I₁ ) = 60°(vì hai góc đối đỉnh)

Xét ΔBIE và ΔBIK, ta có

∠(B₂ ) = ∠(B₁ ) (gt)

BI cạnh chung

∠(I₂ ) = ∠(I₁ ) = 60°

Suy ra: ΔBIE = ΔBIK (g.c.g)

IK = IE (hai cạnh tương ứng)     (1)

Xét ΔCIK và ΔCID, ta có

∠(C₂ ) = ∠(C₁ ) (gt)

CI cạnh chung

∠(I₃ ) = ∠(I₄ ) = 60°

Suy ra: ΔCIK = ΔCID(g.c.g)

IK = ID (hai cạnh tương ứng)     (2)

Từ (1) và (2) suy ra: IE = ID