Bài 55, 56, 57, 58, 59, 60, 61, 62 trang 145 SBT Toán 7 tập 1

Bài 55, 56, 57, 58, 59, 60, 61, 62 trang 145 SBT Toán 7 tập 1

Bài 55: Cho tam giác ABC có ∠B = ∠C Tia phân giác của góc A cắt BC tại D

chứng minh rằng: BD = DC; AB = AC

Lời giải:

Trong ΔADB, ta có:

∠B + ∠(A₁ ) + ∠(D₁) = 180° (tổng 3 góc trong tam giác)

Suy ra: ∠(D₁ ) = 180° - (∠C +(A₁))     (1)

Trong ΔADC, ta có:

∠C +∠(A₂) + ∠(D₂) = 180° (tổng 3 góc trong tam giác)

Suy ra: ∠(D₂) = 180° - (∠C + ∠(A₂) )     (2)

∠B = ∠C (gt)

∠(A₁ ) = ∠(A₂) (gt)

Từ (1) và (2) và gt suy ra: ∠(D₁) = ∠(D₂)

Xét ΔABD và ΔADC, ta có:

∠(A₁ ) = ∠(A₂)(gt)

AD cạnh chung

∠(D₁ ) = ∠(D₂)

Vậy: ΔABD = ΔADC (g.c.g)

Vậy: AB = AC (hai cạnh tương ứng)

DB = DC (hai cạnh tương ứng)

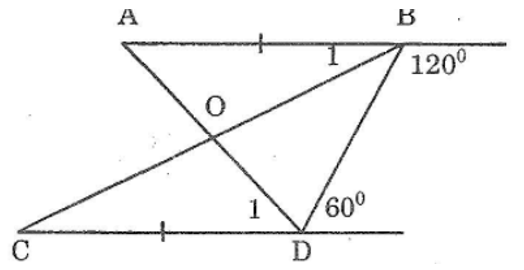
Bài 56: Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC

Lời giải:

Hai đường thẳng AB và CD tạo với BD có hai góc trong cùng phía bù nhau: 120° + 60° = 180°

Suy ra: AB // CD

Ta có: ∠A = ∠(D₁) (hai góc so le trong)

∠C = ∠(B₁) (hai góc so le trong)

AB = CD (gt)

Suy ra: Δ AOB= Δ DOC (g.c.g)

Suy ra: OA = OD; OB = OC (hai cạnh tương ứng)

Vậy O là trung điểm của mỗi đoạn thẳng AD và BC

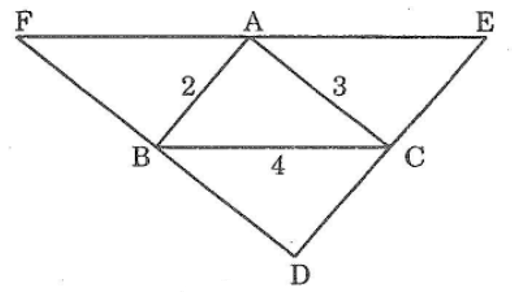
Bài 57: Cho hình dưới trong đó DE // AB, DF // AC, EF // BC. Tính chu vi tam giác DFE

Lời giải:

Xét ΔABC và ΔABF, ta có:

∠(ABC) = ∠(BAF) (so le trong)

AB cạnh chung

∠(BAC) = ∠(ABF) (so le trong)

Suy ra: ΔABC = ΔABF(g.c.g)

Suy ra: AF = BC = 4 (hai cạnh tương ứng)

BF = AC = 3(hai cạnh tương ứng)

Xét ΔABC và ΔACE, ta có:

∠(ACB) = ∠(CAE) (so le trong)

AC cạnh chung

∠(BAC) = ∠(ECA) (so le trong)

Suy ra: ΔABC = ΔCEA(g.c.g)

Suy ra: AE = BC = 4(hai cạnh tương ứng)

CE = AB (hai cạnh tương ứng)

Xét ΔABC và ΔDCB, ta có:

∠(ACB) = ∠(DBC) (so le trong)

BC cạnh chung

∠(ABC) = ∠(DCB) (so le trong)

Suy ra: ΔABC= ΔDCB(g.c.g)

Suy ra: DC = AB = 2(hai cạnh tương ứng)

DB = AC (hai cạnh tương ứng)

Ta có: EF = AE = AF = 4 + 4 = 8

DF = DB + BF = 3+ 3 = 6

DE = DC + CE = 2 + 2 = 4

Vậy chu vi ΔDEF là:

DE + DF + EF = 4+ 6 + 8 = 18 (đơn vị độ dài)

Bài 58: Cho đoạn thẳng AB. Qua A vẽ đường thẳng m vuông góc với AB. Qua B vẽ đường thẳng n vuông góc với AB. Qua trung điểm O của AB vẽ một đường thẳng cắt m ở C và cắt n ở D. so sánh các độ dài OC và OD.

Lời giải:

Xét ΔAOC và ΔBOD ta có:

∠(CAO) = ∠(DBO) = 90°

OA = OB

∠(AOC) = ∠(BOD)

Suy ra: ΔAOC = ΔBOD(g.c.g)

Vậy: OC = OD

Bài 59: Cho tam giác ABC có AB = 2,5cm, AC = 3 cm; BC = 3,5 cm. Qua A vẽ đươnhg thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau tại D. tính chu vi tam giác ACD.

Lời giải:

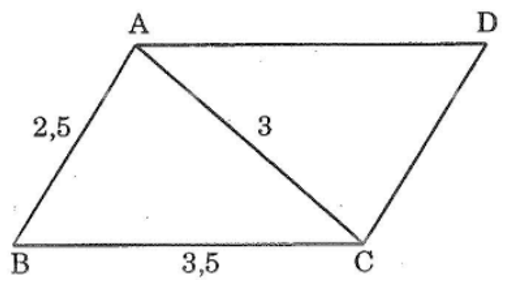
Ta có: AB // CD (gt)

Suy ra ∠(ACD) = ∠(CAB) (hai góc so le trong)

BC // AD (gt)

Suy ra: ∠(CAD) = ∠(ACB) (hai góc so le trong)

Xét ΔABC và ΔCDA, ta có:

∠(CAD) = ∠(ACB) (chứng minh trên)

AC cạnh chung

∠(ACD) = ∠(CAB) (chứng minh trên)

Suy ra: ΔABC = ΔCDA (g.c.g)

Suy ra: CD = AB = 2,5cm và AD = BC = 3,5 cm

Chu vi ΔACD là : AC + AD + CD = 3 + 3,5 + 2,5 = 9 cm

Bài 60: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. kẻ DE vuông góc vớ BC. Chứng minh rằng AB = BE

Lời giải:

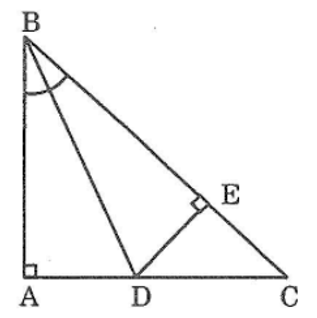
Xét hai tam giác vuông ABD và EBD, ta có:

∠(BAD) = ∠(BED) = 90°

Cạnh huyền BD

∠(ABD) = ∠(EBD) (gt)

Suy ra: Δ ABD = Δ EBD(cạnh huyền, góc nhọn)

Vậy BA = BE ( hai cạnh tương ứng)

Bài 61: Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy.

Chứng minh rằng:

a, ΔBAD = ΔACE

b, DE = BD + CE

Lời giải:

a, Ta có: ∠(BAD) +∠(BAC) +∠(CAE) = 180° (kề bù)

Mà ∠(BAC) = 90° (gt) ⇒ ∠(BAD) +∠(CAE) = 90°         (1)

Trong ΔAEC, ta có: ∠(ACE) = 90° ⇒ ∠(CAE) +∠(ACE) = 90°         (2)

Từ (1) và (2) suy ra: ∠(BAD) = ∠(ACE)

Xét hai tam giác vuông AEC và BDA, ta có:

∠(AEC) + ∠(DBA) = 90°

AC = AB (gt)

∠(ACE) + ∠(BAD) (chứng minh trên)

Suy ra: ΔAEC = ΔBDA(cạnh huyền. Góc nhọn)

b, Ta có: ΔAEC = ΔBDA

⇒ AE = BD và EC = DA

Mà DE = DA + AE

Vậy: DE = CE + BD

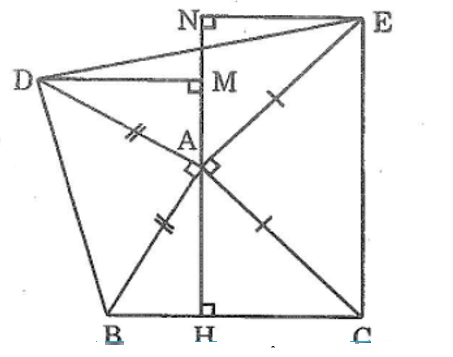
Bài 62: Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH.

Chứng minh rằng:

a. DM = AH

b. MN đi qua trung điểm của DE

Lời giải:

a, Ta có: ∠(BAH) +∠(BAD) +∠(DAM) = 180° (kề bù)

Mà ∠(BAD) =90°⇒ ∠(BAH) + ∠(DAM) = 90°     (1)

Trong tam giác vuông AMD, ta có:

∠(AMD) = 90° ⇒ ∠(DAM) + ∠(ADM) = 90°     (2)

Từ (1) và (2) suy ra: ∠(BAH) = ∠(ADM)

Xét hai tam giác vuông AMD và BHA, ta có:

∠(BAH) = ∠(ADM)

AB = AD (gt)

Suy ra: ΔAMD = ΔBHA(cạnh huyền, góc nhọn)

Vậy: AH = DM (hai cạnh tương ứng)     (3)

b, Ta có: ∠(HAC) + ∠(CAE) +∠(EAN) = 180° (kề bù)

Mà ∠(CAE) = 90° ⇒ ∠(HAC) + ∠(EAN) = 90°(kề bù)     (4)

Trong tam giác vuông AHC, ta có:

∠(AHC) = 90° ⇒ ∠(HAC) + ∠(HCA) = 90°     (5)

Từ (4) và (5) suy ra: ∠(HCA) = ∠(EAN)

Xét hai tam giác vuông AHC và ENA, ta có:

∠(AHC) = ∠(EAN) = 90°

AC = AE (gt)

∠(HCA) = ∠(EAN)

Suy ra : ΔAHC = ΔENA (cạnh huyền, góc nhọn)

Vậy AH = EN (hai cạnh tương ứng)

Từ (3) và (6) suy ra: DM = EN

Vì DM ⇒ AH và EN ⇒ AH nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)

Gọi O là giao điểm của MN và DE

Xét hai tam giác vuông DMO và ENO, ta có:

∠(DMO) = ∠(ENO) = 90°

DM = EN (gt)

∠(MDO) = ∠(NEO)(so le trong)

Suy ra : ΔDMO = ΔENO(g.c.g)

⇒ D = OE

Vậy MN đi qua trung điểm của DE