Bài 70, 71 trang 50 SBT Toán 7 tập 2

Bài 70, 71 trang 50 SBT Toán 7 tập 2

Bài 70: Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?

Lời giải:

Vì tam giác ABC vuông tại B nên AB ⊥ BC.

Suy ra AB là đường cao kẻ từ đỉnh A và CB là đường cao kẻ từ đỉnh C.

Vì B là giao điểm của 2 đường cao AB và CB nên B là trực tâm của tam giác ABC.

Bài 71: Cho hình bên

a. Chứng minh: CI ⊥ AB

b. Cho ∠(ACB)= 40°. Tính ∠(BID), ∠(DIE).

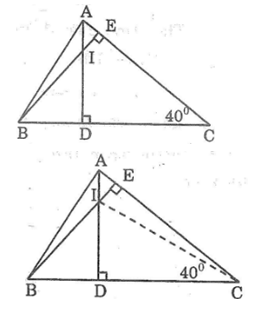
Lời giải:

a. Trong ΔABC ta có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của ΔABC

Suy ra: CI là đường cao thứ ba.

Vậy CI ⊥ AB.

b. Trong tam giác BEC có ∠(BEC) = 90°

⇒ ∠(EBC) + ∠C = 90° (tính chất tam giác vuông)

⇒ ∠(EBC) = 90° - ∠C = 90° - 40° = 50° hay ∠(IBD)= 50°

Trong tam giác vuông IDB có ∠(IDB) = 90°

⇒ ∠(IBD) + ∠(BID) = 90° (tính chất tam giác vuông)

⇒ ∠(BID) = 90° - ∠(IBD) = 90° - 50° = 40°

Mà ∠(BID) + ∠(DIE) = 180° (2 góc kề bù)

Nên ∠(DIE) = 180° - ∠(BID)= 180° - 40° = 140°.