Bài 72, 73, 74, 75, 76, 77, 78, 79, 80, 81 trang 51 SBT Toán 7 tập 2
Bài 72, 73, 74, 75, 76, 77, 78, 79, 80, 81 trang 51 SBT Toán 7 tập 2
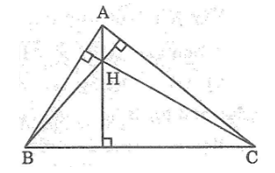
Bài 72: Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC.
Lời giải:
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC, BH ⊥ AC, CH ⊥ AB
Trong ΔAHB, ta có:
AC ⊥ BH
BC ⊥ AH
Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
AB ⊥ CH
CB ⊥ AH
Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
BA ⊥ HC
CA ⊥ BH
Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.
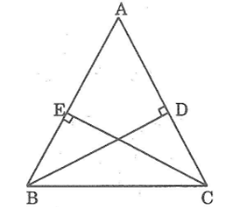
Bài 73: Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng đó là tam giác cân
Lời giải:
Xét hai tam giác vuông BDC và CEB, có:
∠(BDC) = ∠(CEB) = 90°
BD = CE (gt)
BC cạnh huyền chung
Suy ra: ΔBDC = ΔCEB
(cạnh huyền, cạnh góc vuông)
Suy ra: ∠(DCB) = ∠(EBC)
(hai góc tương ứng bằng nhau)
Hay ∠(ACB) = ∠(ABC)
Vậy ΔABC cân tại A.
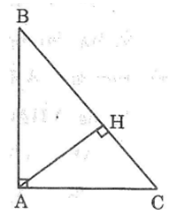
Bài 74: Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
Lời giải:
*Tam giác ABC có ∠(BAC) = 90°
Vì CA là đường cao xuất phát từ đỉnh B nên giao điểm của hai đường này là A.
Vậy A là trực tâm của ΔABC.
*Tam giác AHB có ∠(AHB) = 90°
Vì AH là đường cao xuất phát từ đỉnh A, BH là đường cao xuất phát từ đỉnh B nên giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHB.
*Tam giác AHC có ∠(AHC) = 90°
Vì AH là đường cao xuất phát từ đỉnh A, CH là đường cao xuất phát từ đỉnh C nên giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHC.
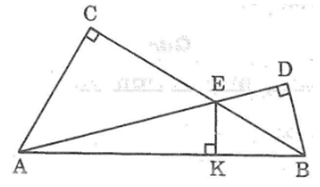
Bài 75: Cho hình dưới. Có thể khẳng định rằng các đường thẳng AC, BD, KE cùng đi qua một điểm hay không? Vì sao?
Lời giải:
Trong ΔAEB, ta có: AC ⊥ EB
Suy ra AC là đường cao xuất phát từ đỉnh A.
Trong ΔAEB, ta có: BD ⊥ AE
Suy ra BD là đường cao xuất phát từ đỉnh B.
Trong ΔAEB, ta có: EK ⊥ AB
Suy ra EK là đường cao xuất phát từ đỉnh E
Theo tính chất ba đường cao trong tam giác nên các đường thẳng AC, BD và EK cùng đi qua một điểm.
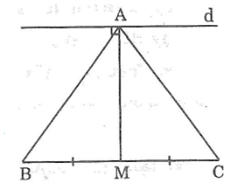
Bài 76: Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua A kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC.
Lời giải:
Vì ΔABC cân tại A và AM là đường trung tuyến nên AM cũng là đường cao
Ta có: AM ⊥ BC
d ⊥ AM (gt)
Vì hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song nhau nên ta có: d // BC.
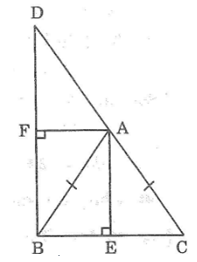
Bài 77: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ΔABC, đường cao AF của ΔACD. Chứng minh rằng ∠(EAF) = 90°.
Lời giải:
Ta có: ΔABC cân tại A
AE ⊥ BC (gt)
Vì AE là đường cao của tam giác ABC nên AE cũng là đường phân giác của ∠(BAC)
Lại có: ΔADB cân tại A
AF ⊥ BD (gt)
Vì AF là đường cao nên AF cũng là đường phân giác của ∠(BAD)
Mà ∠(BAC) và ∠(BAD) là hai góc kề bù nên: AE ⊥ AF.
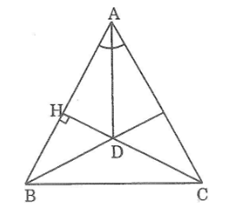
Bài 78: Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.
Lời giải:
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ΔABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
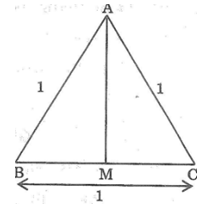
Bài 79: Tam giác ABC có AB = AC = 13cm, BC = 10cm. Tính độ dài đường trung tuyến AM.
Lời giải:
Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao.
Suy ra: AM ⊥ BC
Ta có: MB = MC = 1/2 BC = 1/2 .10 = 5 (cm)
Trong tam giác vuông AMB có (AMB) = 90°
Áp dụng định lý Pitago ta có:
AB2 = AM2 + MB2
Suy ra: AM2 = AB2 - MB2
= 132 - 52 = 169 - 25 = 144
Vậy AM = 12(cm)
Bài 80: Cho tam giác ABC có ∠B , ∠C là các góc nhọn, AC > AB. Kẻ đường cao AH. Chứng minh rằng ∠(HAB) < ∠(HAC) .
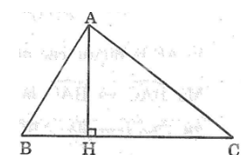
Lời giải:
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90°
Suy ra: ∠B + ∠(HAB) = 90° (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90°
Suy ra: ∠C + ∠(HAC) = 90° (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Bài 81: Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (hình dưới)
a. Chứng minh rằng A là trung điểm của EF.
b. Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
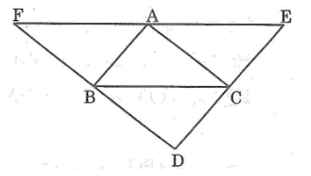
Lời giải:
Xét ΔABC và ΔACE, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔACE (g.c.g)
⇒ AE = BC (1)
Xét ΔABC và ΔABF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.
b. Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.

