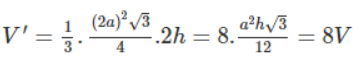Bài IV.1, IV.2, IV.3 trang 158 SBT Toán 8 tập 2
Bài IV.1, IV.2, IV.3 trang 158 SBT Toán 8 tập 2
Bài IV.1 trang 158 sách bài tập Toán 8 Tập 2: Quan sát hình lăng trụ đứng tam giác ở hình bs.15 rồi điền số thích hợp vào các ô trống trong bảng sau:
| a | 9 | 20 | 63 | ||
| b | 40 | 12 | 45 | ||
| c | 37 | 65 | |||
| d | 8 | 13 | |||
| Diện tích một đáy | 210 | ||||
| Diện tích xung quanh | 1512 | ||||
| Diện tích toàn phần | 4464 | ||||
| Thể tích | 3570 | 8190 |
Lời giải:
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| d | 8 | 18 | 17 | 24 | 13 |
| Diện tích một đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |
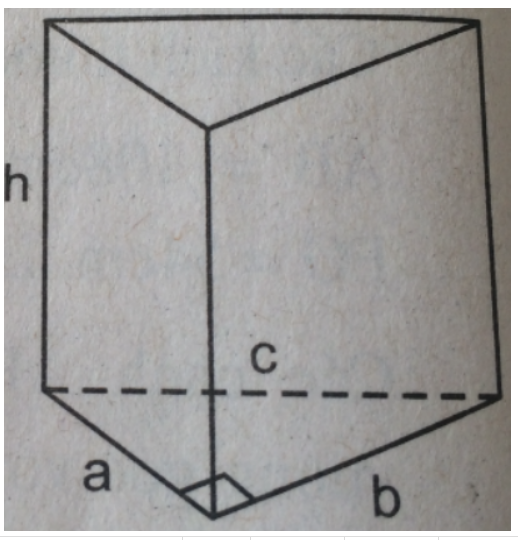
Bài IV.2 trang 158 sách bài tập Toán 8 Tập 2: Một con kiến đang ở vị trí M là trung điểm cạnh A'D' của một chiếc hộp hình lập phương ABCD.A'B'C'D' (h. bs.16). Con kiến muốn bò qua sáu mặt của chiếc hộp rồi quay trở về M. Tìm đường đi ngắn nhất của con kiến.
Lời giải:
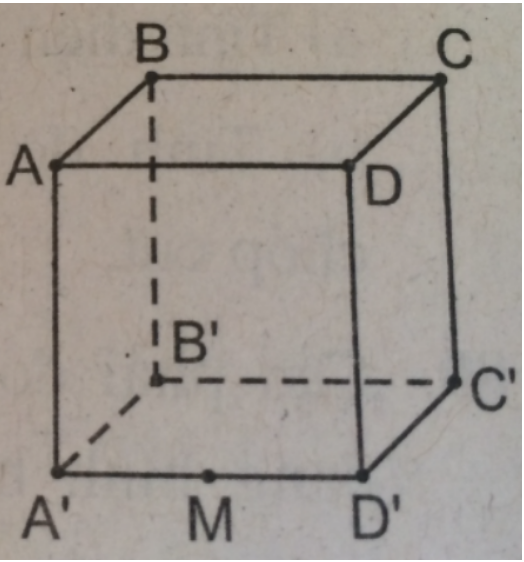
Trải 6 mặt của hình lập phương ABCD.A'B'C'D' như hình bs.18a. Để đi đường ngắn nhất từ M đến M' (M' chính là trung điểm của A'D' trên mặt khai triển) thì con kiến cần bò theo đoạn thẳng MM'. Trên chiếc hộp, đường đi ngắn nhất của con kiến là đường MNPQKZM' như ở hình bs.18b (dễ thấy N, P, Q, K, Z lần lượt là trung điểm của DD', CD, BC, BB', A'B').
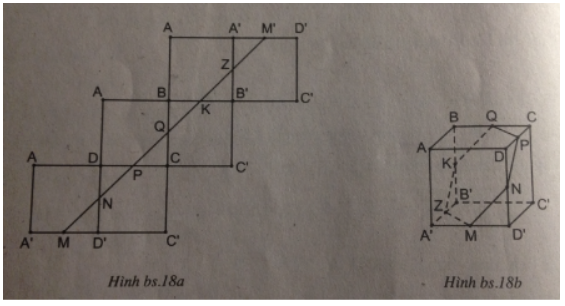
Bài 3 trang 158 sách bài tập Toán 8 Tập 2: Thể tích của một hình chóp tam giác đều thay đổi thế nào nếu ta tăng
a. Gấp đôi chiều cao của hình chóp;
b. Gấp đôi cạnh đáy của hình chóp;
c. Gấp đôi cả chiều cao và cạnh đáy của hình chóp.
Lời giải:
Tam giác đều cạnh a có diện tích bằng (√3a2)/4. Do đó, hình chóp tam giác đều với cạnh đáy a, chiều cao h có thể tích :
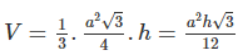
a. Nếu tăng gấp đôi chiều cao thì thể tích hình chóp là:
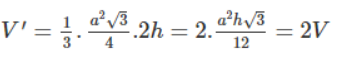
b. Nếu tăng gấp đôi cạnh đáy thì thể tích hình chóp là:
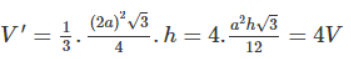
c. Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là: