Bài 86, 87, 88, 89, 90 trang 157 SBT Toán 8 tập 2

---

Bài 86, 87, 88, 89, 90 trang 157 SBT Toán 8 tập 2

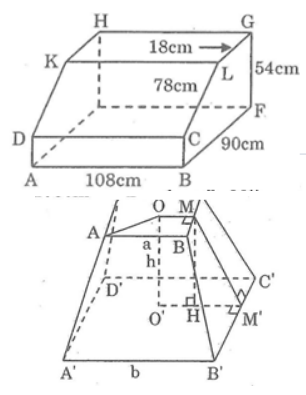
Bài 86 trang 157 sách bài tập Toán 8 Tập 2: Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng như hình vẽ các kích thước của nó là: AB= 108cm,BC =24cm; BF = 90 cm, FH =54 cm, LG=18 cm, LC = 78cm.Các cạnh AB,DC,EF,HG và KL đều vuông góc với mặt phẳng (ADKHE) và LG song song với BF.Hãy tính:

a. Diện tích hình chữ nhật CDKL

b. Diện tích hình thang BCLGF

c. Thể tích hình lăng trụ đứng ADKHE.BCLGF

Lời giải:

a. Diện tích hình chữ nhật CDKL

CD = AB = 108 cm

S_CDKL = CD.CL = 108.78 = 8424 (cm²)

b. Hình BCLGF có thể chia thành hai hình Một hình chữ nhật có kích thước 18cm và 54cm, một hình thang vuông có: 2 đáy là 24cm và 54cm, chiều cao 72cm

Diện tích phần hình chữ nhật là: S = 18.54= 972(cm²)

Diện tích phần hình thang vuông

S = [(24 + 54) : 2].72 = 2808 (cm²)

Diện tích hình BCLGF bằng: 972 + 2808 = 3780 (cm²)

c. Hình lăng trụ đứng ADKHE.BCLGF có thể chia thành hai hình.

Một hình hộp chữ nhật có hai cạnh đáy là 13cm và 54cm ,chiều cao hình hộp 108cm, một hình lăng trụ đứng đáy hình thang vuông với hai cạnh đáy 24cm và 54cm, chiều cao đáy 72cm chiều cao lăng trụ 108cm

Thể tích phần hình hộp chữ nhật là :

V = 18.54.108 = 104976 (cm³)

Thể tích phần hình lăng trụ đứng là:

V = S.h = 2808.108 = 303264 (cm³)

Thể tích lăng trụ đứng ADKHE.BCLGF bằng:

V = 104976 +303264 = 408240 (cm³)

Bài 87 trang 157 sách bài tập Toán 8 Tập 2: Thể tích của hình chóp đều là 126 cm³,chiều cao hình chóp là 6cm.Như vậy trong các số dưới đây ,số nào là diện tích đáy của nó?

A.45(cm²)

B.52(cm²)

C.63(cm²)

D,60(cm²)

E.50(cm²)

Lời giải:

Ta có: V = 1/3 .S.h mà V = 126 (cm³) ,h = 6cm nên :

126 = 1/3 .S.6 ⇒ S = 126 :2 = 63 (cm²)

Vậy chọn đáp án C

Bài 88 trang 157 sách bài tập Toán 8 Tập 2: Cho hình chóp cụt đều ABCD.A'B'C'D' có cạnh đáy là a và 2a chiều cao của mặt bên là a

a.Tính diện tích xung quanh hình chóp cụt

b.Tính độ dài cạnh bên và chiều cao hình chóp cụt

Lời giải:

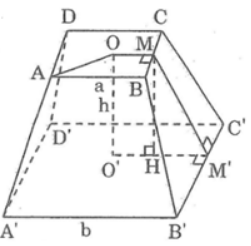
Một mặt bên của hình chóp cụt là một hình thang có hai đáy là a và 2a; đường cao bằng a.

Diện tích mặt bên là:

S = (a+ 2a): 2.a =3/2 a² (đvtt)

Diện tích xung quanh hình nón cụt:

S_xq = 4.3/2 a² = 6a² (đvtt)

Kẻ A'H ⊥ AB.

Ta có K là trung điểm của AB, I là trung điểm của A'B'. O và O' là tâm của hai hình vuông đáy.

Ta có: A'I =a/2 ; AK = a ⇒ AH =a/2

Áp dụng định lí Pi-ta-go vào tam giác vuông AA'H, ta có:

A'A² = A'H² + AH² = a² +a²/4 = 5a²/4

Suy ra: AA' = √(5a²/4)

Kẻ IE ⊥ OK, ta có: OK = a ⇒ EK = a/2

Áp dụng định lí Pi-ta-go vào tam giác vuông IEK, ta có:

IK² = IE² + EK²

Suy ra: IE² = IK² - EK² = a² – (a/2 )² =3a²/4

Vậy IE = √(3a²/4)

Bài 89 trang 157 sách bài tập Toán 8 Tập 2: Cần phải đo đường chéo của một viên gạch có dạng hình hộp chữ nhật mà chỉ được phép sử dụng thước có chia vạch thì phải làm như thế nào?

Lời giải:

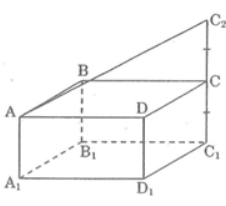
Gọi viên gạch là hình hộp chữ nhật ABCD.A₁B₁C₁D₁.

Để đo đường chéo AC₁ ta làm như sau: trên tia đối tia CC₁ ta lấy điểm C₂ sao cho CC₂ = CC₁.

Dùng thước chia vạch đo đoạn AC₂. Độ dài đoạn AC₂ chính là độ dài đường chéo AC₁.

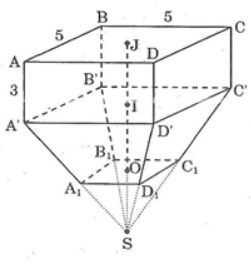
Bài 90 trang 157 sách bài tập Toán 8 Tập 2: Tính thể tích của 1 trụ bê tông cho theo các kích thước ở hình, SJ = 9, OI = IJ. Phần trên là một hình hộp chữ nhật, phần dưới là một hình chóp cụt đều.

Lời giải:

Thể tích phần hình hộp chữ nhật:

V = 5.5.5 = 75 (đvtt)

Ta có: IJ = AA' ⇒ IJ = 3

OI = IJ = 3

SJ = 9 ⇒ SO = 3

Suy ra: SA₁ = A₁A'; SD₁ = D₁D'

Khi đó hình vuông A₁B₁C₁D₁ có cạnh A₁ B₁ = 1/2 A'B' = 2,5

Thể tích hình chóp đều S. A'B'C'D' là:

V= 1/3 (5.5).6 = 50 (đvtt)

Thể tích hình chóp đều A₁B₁C₁D₁ là:

V= 1/3(2,5.2,5).3 = 6,25 (đvtt)

Thể tích hình chóp cụt A'B'C'D'.A₁B₁C₁D₁ là:

V = 50 – 6,25 = 43,75 (đvtt)

Thể tích của một trụ bê tông là:

V = 43,75 + 75 = 118,75 (đvtt).