Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau

Ôn tập chương II

Bài 8 (trang 78 sgk Hình học 11 nâng cao): Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = k.BN (k > 0 cho trước)

a) Chứng minh rằng MN song song với một mặt phẳng cố định

b) Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = k.IN

Lời giải:

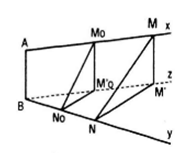
b) Thuận. Gọi O là một điểm thuộc đọa AB sao cho OA : OB = k , từ O ta vẽ hai tia Ox’ và Oy’ sao cho Ox’//Ax, Oy’//By. Xét phép chiếu song song theo phương AB lên mp(Ox’, Oy’). Gọi M’, N’ lần lượt là hình chiếu của M và N theo phép chiếu này . Khi đó giao điểmcủa MN và M’N’ chính là điểm I vì rõ ràng ta có :

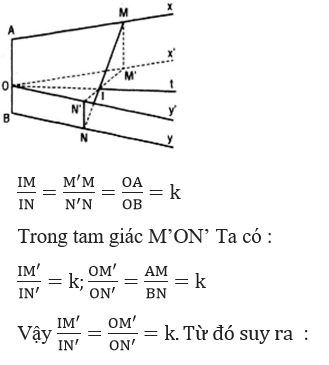
I phải nằm trên tia phân giác Ot của góc x’Oy’.

Đảo. Giả sử I là một điểm bất kì thuộc tia phân giác Ot của góc x’Oy’. Gọi M’, N’ là những điểm lần lượt thuộc tia Ox’, tia Oy’ sao cho M’, I , N’ thẳng hàng và (IM^')/(IN^' )=k (có thể tìm M’, N’ bằng cách dùng phép vị tự tâm I tỉ số -k trên mp(Ox’y’)). Gọi M, N lần lượt là những điểm thuộc các tia Ax, By sao cho AM = OM’, BN = ON’. Dễ thấy I, M, N thẳng hàng và IM : IN = k

Kết luận : Tập hợp các điểm I thỏa mãn điều kiện bài toán là tia phân giác Ot của góc x’Oy’.