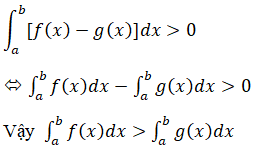Chứng minh rằng nếu f(x) > 0 trên [a; b] thì

Bài 3: Tích phân

Haylamdo biên soạn và sưu tầm lời giải Bài 13 trang 153 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 13 (trang 153 sgk Giải Tích 12 nâng cao):

a) Chứng minh rằng nếu f(x) > 0 trên [a; b] thì

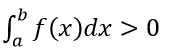
b) Chứng minh rằng nếu f(x) > g(x) trên [a; b] thì

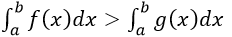
Lời giải:

a) Gọi F(x) là một nguyên hàm của f(x) trên đoạn [a; b]. , ta có: F’(x) = f(x) > 0 trên đoạn [a; b]. do đó F(x) tăng trên đoạn [a; b]

Vì vậy a < b => F(a) < F (b)

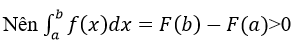
b) Trên đoạn [a, b ] ta có; f(x) > g(x) nên f(x ) – g(x) > 0. Theo câu a, ta có: f(x ) – g(x) > 0, nên