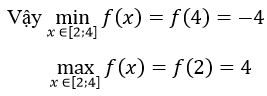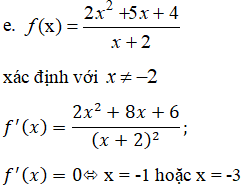Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: f(x) = x^2 + 2x - 5 trên đoạn [-2;3]

Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Haylamdo biên soạn và sưu tầm lời giải Bài 17 trang 22 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 17 (trang 22 sgk Giải Tích 12 nâng cao):Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

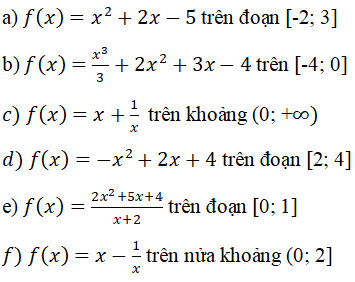
Lời giải:

a) Hàm số f(x)= x² + 2x – 5

Tập xác định D = R.

Đạo hàm y’= 2x +2 = 0 ⇔ x = - 1

Cách 1. Bảng biến thiên:

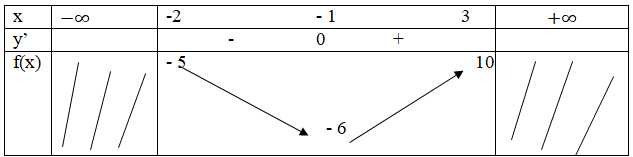
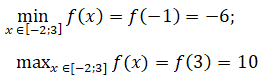
Cách 2, ta có: f(-2) = -5; f(-1) = -6; f(3) = 10

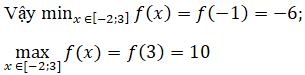
b.Hàm số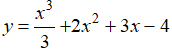

Hàm số đã cho xác định trên R

f' (x)=x²+4x+3; f'(x)=0 ⇔ x = -1 hoặc x = -3

Ta có: f(-4) = -16/3; f(-3)=-4; f(-1)=-16/3; f(0)=-4

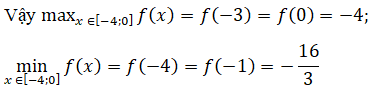
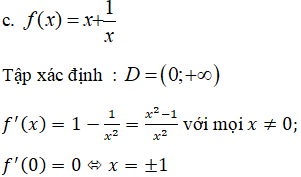
Bảng biến thiên:

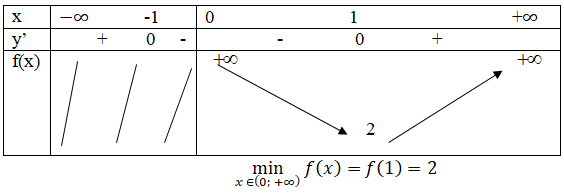
Hàm số không đạt giá trị lớn nhất trên (0; +∞)

d. Hàm số y = - x² +2x + 4

Hàm số liên tục trên R.

f' (x)= -2x+2; f'(x)=0 ⇔ x = 1 (loại vì x = 1 không thuộc [2;4])

Ta có: f(2)=4; f(4)=-4