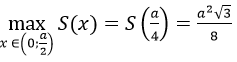Cho tam giác đều ABC cạnh a. người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC

Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Haylamdo biên soạn và sưu tầm lời giải Bài 19 trang 22 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 19 (trang 22 sgk Giải Tích 12 nâng cao): Cho tam giác đều ABC cạnh a. người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trị của điểm M sao cho hình chữ nhật có diện tích lớn nhất và giá trị lớn nhất đó là.

Lời giải:

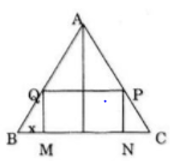
Đặt BM = x (0<x<a/2)

Ta có: MN = a – 2x; QM = BM.tan B =x √3

Diện tích hình chữ nhật MNPQ là:

S(x)=QM.MN=x √3(a-2x)

S(x)=√3(ax-2x²)

Bài toán trở thành tìm giá trị lớn nhất của S(x) trên khoảng (0; a/2)

Ta có S' (x)=√3 (a-4x);S' (x)=0 <=> x=a/4

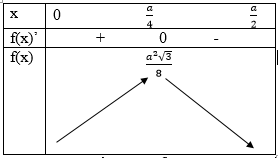
S đạt giá trị lớn nhất tại x=a/4 và giá trị lớn nhất của diện tích hình chữ nhât MNQP là: