Hỏi công thức Viet về Phương trình bậc hai với hệ số thực có còn đúng cho Phương trình bậc hai

Bài 2: Căn bậc hai của số phức và phương trình bậc hai

Haylamdo biên soạn và sưu tầm lời giải Bài 20 trang 196 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 20 (trang 196 sgk Giải Tích 12 nâng cao):

a) Hỏi công thức Viet về Phương trình bậc hai với hệ số thực có còn đúng cho Phương trình bậc hai với hệ số phức không? Vì sao?

b) Tìm hai số phức, biế tổng của chúng bằng 4 – I và tích của chúng bằng 5(1 – i).

c) Có phải mọi phương trình bậc hai z²+Bx+C=0 (B, C là hai số phức nhận hai nghiệm là hai số phức liên hợp không thực phải có các hệ số B, C là hai số thực? vì sao? Điều ngược lại có đúng không?

Lời giải:

a) Định lí Viet vẫn đúng cho phương trình bậc hai với hệ số phức,

Giả sử Phương trình: Az²+Bz+C=0 (A ≠ 0;A,B,C ∈C) có hai nghiệm:

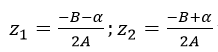
với α là một căn bậc hai của biệt số Δ=B²-4AC

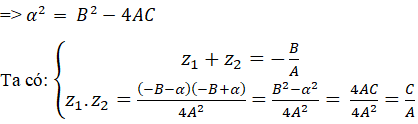
b) Theo định lí Viet thì hai số phức cần tìm là nghiệm của phương trình:

z²-(4-i)z+5(1-i)=0 (*)

Ta có Δ=(4-i)²-20(1-i)=-5+12i

Δ là một căn bậc hai là α=2+3i, nên (*) có hai nghiệm là:

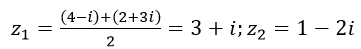
Vậy hai số cần tìm là: 3+i;1-2i

c) Giả sử phương trình: z²+Bz+C=0 nhận hai nghiệm là hai số phức liên hợp không thực sau đây: z₁=a+bi;z₂=a-bi với b ≠ 0;a.b ∈R

Vì z₁;z₂ là nghiệm Phương trình: z²+Bz+C=0 nên ta có:

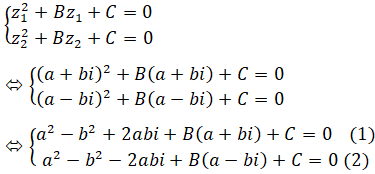
Cộng vế với vế của (1) và (2) ta được:

2a²-2b²+2aB+2C=0 ⇔ a²- b²+aB+C=0 => C=b²-(a²+aB) (*)

Thay vào (1) ta được:

(1) ⇔ a²-b²+2abi+B(a+bi)+ b²-(a²+aB)=0

⇔ 2abi+bBi=0 (vì b≠0)

⇔ B=-2a (**)

Từ (*) và(**) suy ra, B và C là 2 số thực . Nên khẳng định là đúng.

- Điều ngược lại. nếu B, C là hai số thực thì Phương trình z²+Bz+C=0 nhận hai nghiệm số phức liên hợp là sai, chẳng hạn Phương trình z²+2z-3=0 có nghiệm là z = 1; z =-3