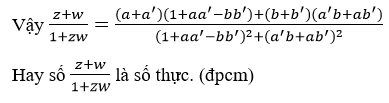Chứng minh rằng nếu trang 209 sgk Giải Tích 12 nâng cao

Câu hỏi và bài tập ôn tập chương 4

Haylamdo biên soạn và sưu tầm lời giải Bài 38 trang 209 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 38 (trang 209 sgk Giải Tích 12 nâng cao): Chứng minh rằng nếu

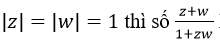
là số thực (giả sử 1 zw ≠ 0

Lời giải:

Giả sử z=a+bi,w=a'+b'i với a²+b²=a'²+b'²=1 và 1+zw ≠ 0

Vì |z| = 1 nên z.z−=1

Khi đó, ta có:

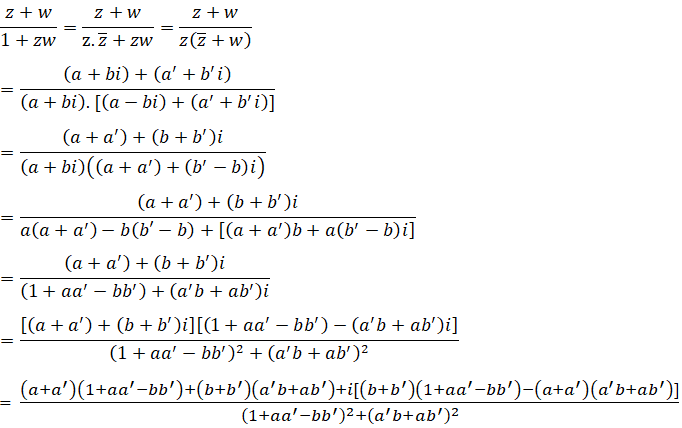
Xét phần ảo ở trên tử số ta có: (b+b' )(1+aa'-bb' )-(a+a' )(a' b+ab' )

=b+baa'-b²b'+b'+b' aa'-bb'²-aa' b-a² b'-a'² b-a'ab'

=b+b'-b' (a²+b² )-b(b'²+a'² )=b+b'-b'-b=0