Khảo sát và vẽ đồ thị hàm số y=x^3+3x^2-4
Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
Haylamdo biên soạn và sưu tầm lời giải Bài 40 trang 43 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 40 (trang 43 sgk Giải Tích 12 nâng cao):
a) Khảo sát và vẽ đồ thị hàm số y=x3+3x2-4
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.
c) Chứng minh rằng điểm uốn làm tâm đối xứng của đồ thị.
Lời giải:
a) TXĐ: R
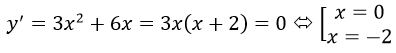
y'>0 trên khoảng (-∞; -2)và (0; +∞)
y'<0 trên khoảng (-2; 0)
+ yCĐ = y(-2) = 0; yCT = y(0) = -4
+ limx→-∞y = -∞; limx→+∞ y = +∞
+ y'' = 6x+6 = 6(x+1) = 0 ⇔ x = -1
Bảng xét dấu y’’
| X | -∞ | -1 | +∞ | ||
| Y’’ | - | 0 | + | ||
| Đồ thị | Lồi | điểm uốn U(-1; -2) | lõm |
Hàm số lồi trên khoảng (-∞; -1)
Hàm số lõm trên khoảng (-1; +∞)
Hàm số có 1 điểm uốn U(-1; -2)
Bảng biến thiên:
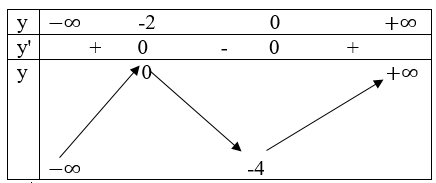
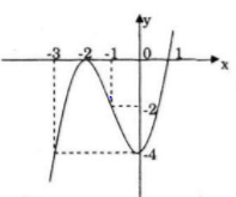
Đồ thị
Đi qua điểm (1; 0) và (-3; -4)
b) Hàm số y = x3+3x2-4 có điểm uốn U(-1; -2)
Ta có: y' = 3x2 + 6x; y’(-1) = -3
Phương trình tiếp tuyến tại điểm uốn U(-1; -2) có dạng
y-y0=y'(x0)(x-x0)
⇔ y+2=-3(x+1)
⇔ y=-3x-5
Vậy phương trình tiếp tuyến tại điểm uốn là: y = -3x - 5.
c) Cách 1. Đồ thị nhận U(-1; -2) là tâm đối xứng khi và chỉ khi:
f(x0+x)+f(x0-x)=2y0 với ∀x
⇔ f(x-1)+f(-x-1)=-4 ∀x
⇔ (x-1)3+3(x-1)2-4+(-1-x)3+3(-1-x)2-4 =-4 ∀x
⇔ x3-3x2+3x-1+3x2-6x+3-4-1-3x-3x2-x3+3+6x+3x2-4=-4 ∀x
⇔ -4 = - 4 ∀ x
⇒ I(-1; -2) là tâm đối xứng của đồ thị.
Cách 2. Gọi U(-1; -2) là tọa độ điểm uốn, tịnh tiến OU giữa các tọa độ cũ.
Theo công thức đổi trục tọa độ
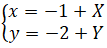
Phương trình trở thành Y = X3-3X đây là hàm số lẻ nên đồ thị nhận điểm uốn làm tâm đối xứng ⇒ điều phải chứng minh.

