Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x - 1/x + 1

Luyện tập (trang 57-58)

Haylamdo biên soạn và sưu tầm lời giải Bài 62 trang 57 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 62 (trang 57 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số:

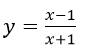
b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.

Lời giải:

a) TXĐ: D = R \ {-1}

Sự biến thiên:

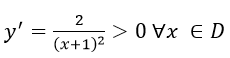
⇒ Hàm số luôn đồng biến trên D.

Giới hạn:

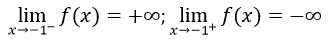
⇒ Đồ thị có 1 tiệm cận đứng là đường thẳng x = -1

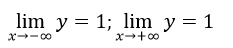
⇒ Đồ thị hàm số nhận đường thẳng y = 1 làm tiệm cận ngang

Bảng biến thiên:

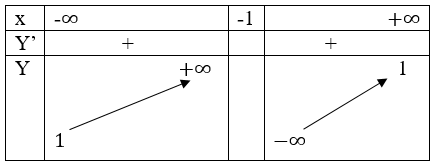
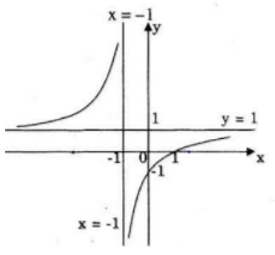
Đồ thị hàm số

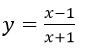
Giao với Ox: (1; 0)

Giao với Oy: (0; -1)

b) Ta có giao điểm của 2 tiệm cận I(-1; 1)

Áp dụng công thức đổi trục

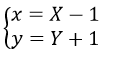
Thay vào hàm số

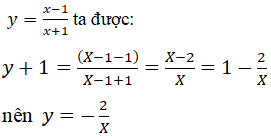
Đây là hàm số lẻ nên đồ thị hàm số đã cho nhận I(-1; 1) làm tâm đối xứng.