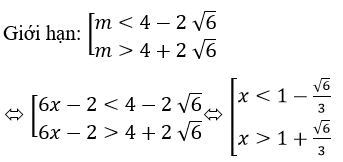Khảo sát tự biến thiên và vẽ đồ thì hàm số: y = 2x^2 - x + 1/x - 1

Luyện tập (trang 57-58)

Haylamdo biên soạn và sưu tầm lời giải Bài 65 trang 58 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 65 (trang 58 sgk Giải Tích 12 nâng cao):

a) Khảo sát tự biến thiên và vẽ đồ thì hàm số:

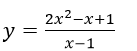
b) Với giá trị nào của m đường thẳng y=m-x cắt đồ thị của hàm số đã cho tại 2 điểm phân biệt?

c) Gọi A và B là 2 giao điểm đó. Tìm tập hợp các trung điểm M của đoạn AB nói trên m thay đổi.

Lời giải:

a) TXĐ: D = R \ {1}

Sự biến thiên:

Đạo hàm:

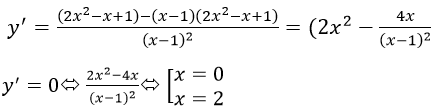
Hàm số đồng biến trên khoảng (-∞; 0) và (2; +∞)

Hàm số nghịch biến trên khoảng (0; 1) và (1; 2).

Hàm số đạt cực đại tại x=0 và y_CĐ = -1.

Hàm số đạt cực tiểu tại x= 2 và y_CT = 7

Giới hạn: lim_x→1⁺⁡ y = +∞; lim_x→1^-⁡y=- ∞

Vậy đồ thị hàm số có 1 tiệm cận đứng là đường thẳng x = 1

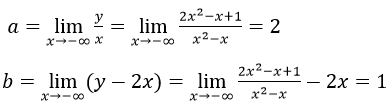
Vậy đồ thị hàm số có 1 tiệm cận xiên là đường thẳng: y=2x+1

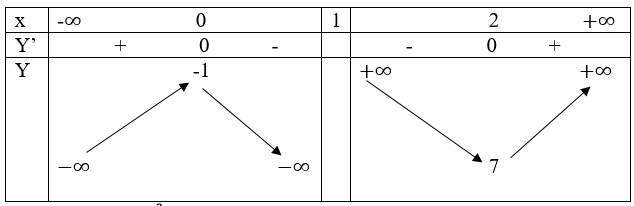
Bảng biến thiên:

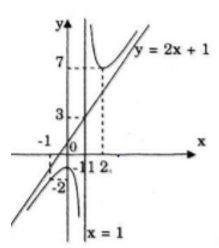
Đồ thị hàm số

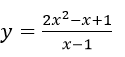
b) Hoành độ giao điểm của đường thẳng y=m-x và đồ thị hàm số nghiệm của Phương trình:

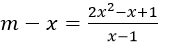
<=> (m-x)(x-1)=2x²-x+1,x ≠ 1

<=> f(x)=3x²-x(2+m)+m+1=0,f(1) ≠ 0

Để đường thẳng (C ) tại 2 điểm phân biệt thì: Δ>0 và f(1) ≠ 0

Ta có: Δ=(2+m)²-4.3(m+1)>0

⇔ m²-8m-8>0

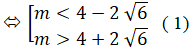
Lại có: f(1) = 2 ≠ 0 với mọi m . (2)

Từ (1) và (2) suy ra, với 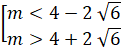thì đường thẳng y = m- x sẽ cắt (C) tại 2 điểm phân biệt A, B.

c) Gọi A(x_A;y_A ),B(x_B,y_B) là hai giao điểm của đường thẳng d và đồ thị (C)

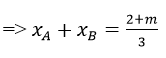
gọi M(x_M;y_M ) là trung điểm của AB

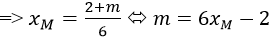
Mà điểm M thuộc đường thẳng y= m- x ( vì đường thẳng AB chính là y = m - x)

⇒ y_M = m – x_M = 6x_M – 2 – x_M = 5x_M – 2

Vậy tập hợp trung điểm M của đoạn AB khi m biến thiên là: y=5x-2