Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0
Toán lớp 12 Bài 2: Cực trị của hàm số
Bài 3 (trang 18 SGK Giải tích 12): Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Lời giải:
Hàm số có tập xác định D = R và liên tục trên R.
+ Chứng minh hàm số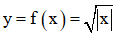 
không có đạo hàm tại x = 0.
Xét giới hạn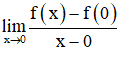 
:
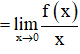
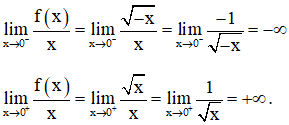
⇒ Không tồn tại giới hạn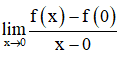 
Hay hàm số không có đạo hàm tại x = 0.
+ Chứng minh hàm số đạt cực tiểu tại x = 0 (Dựa theo định nghĩa).
Ta có : f(x) > 0 = f(0) với ∀ x ∈ (-1 ; 1) và x ≠ 0
⇒ Hàm số y = f(x) đạt cực tiểu tại x = 0.
Kiến thức áp dụng
Hàm số y = f(x) liên tục trên (a ; b) và x0 ∈ (a ; b).
+ Hàm số y = f(x) có đạo hàm tại x0 nếu tồn tại giới hạn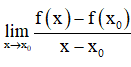 
+ Hàm số y = f(x) đạt cực tiểu tại x0 nếu tồn tại số dương h sao cho f(x) > f(x0) với ∀ x ∈ (x0 – h ; x0 + h) và x ≠ x0.
