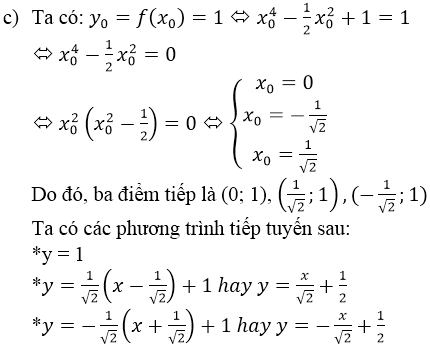Tính a, b để hàm số cực trị bằng 3/2 khi x =1

Toán lớp 12 Ôn tập cuối năm giải tích 12

Bài 5 (trang 146 SGK Giải tích 12): Cho hàm số y = x⁴ + a⁴ + b

a) Tính a, b để hàm số cực trị bằng 3/2 khi x =1.

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi:

a = -1/2, b = 1

c) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.

Lời giải:

a) Đạo hàm y’ = 4x³ + 2ax

Hàm số có cực trị tại x = 1.

⇔ y’(1) = 0

⇔ 4.13 + 2a.1 = 0

⇔ a = -2.

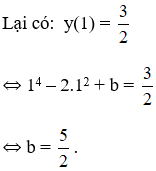
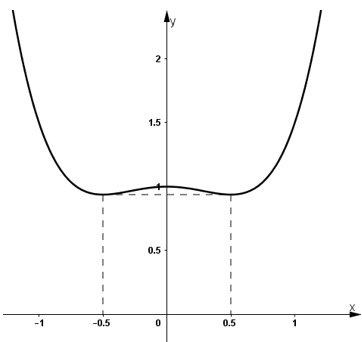
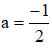
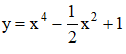
b) Với ; b = 1 thì hàm số trở thành:

- TXĐ: D = R.

- Sự biến thiên:

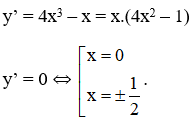
+ Giới hạn:

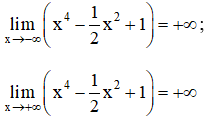
+Bảng biến thiên:

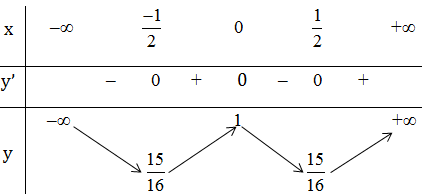
Kết luận: Hàm số đồng biến trên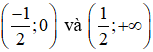

Hàm số nghịch biến trên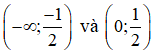

Hàm số đạt cực đại tại x = 0; y_CĐ = 1

Hàm số đạt cực tiểu tại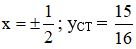

- Đồ thị: