Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau
Toán lớp 12 Bài 3 : Phương trình đường thẳng trong không gian
Bài 5 (trang 90 SGK Hình học 12): Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
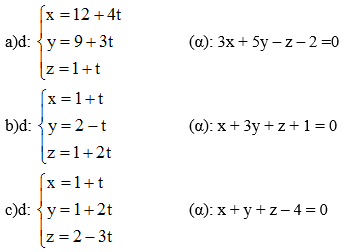
Lời giải:
a) Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
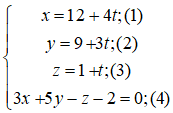
Thay (1); (2); (3) vào (4) ta được:
3(12 + 4t) + 5(9 + 3t) – (1 + t) – 2 = 0
⇔ 36 + 12t + 45 + 15t – 1 – t – 2 = 0
⇔ 26t + 78 = 0
⇔ t = -3
Vậy (d) cắt (α) tại một điểm M(0 ; 0 ; -2).
b) Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
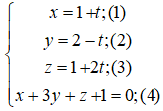
Thay (1); (2); (3) vào (4) ta được:
1 + t + 3(2 – t) + 1 + 2t + 1 = 0
⇔ 0t + 9 = 0
Phương trình vô nghiệm
⇒ (d) không cắt (α).
c) Giao điểm (nếu có) của đường thẳng (d) và mp(α) là nghiệm hệ phương trình:
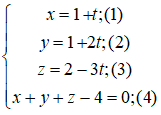
Thay (1); (2); (3) vào (4) ta được:
1 + t + 1 + 2t + 2 – 3t – 4 = 0
⇔ 0t = 0
Phương trình có vô số nghiệm
⇒ (d) ⊂ (α)
hay (d) cắt (α) tại vô số điểm.
Kiến thức áp dụng
+ Trong không gian Oxyz, cho mặt phẳng (α): Ax + By + Cz + D = 0 và đường thẳng d: 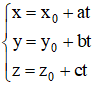
Xét phương trình A(x0 + at) + B(y0 + bt) + C(z0 + ct) + D = 0 (1)
+ Nếu (1) vô nghiệm ⇒ (d) không có điểm chung với (α) ⇒ d // (α).
+ Nếu (1) có 1 nghiệm t = t0 thì (d) cắt (α) tại M (x0 + at0; y0 + bt0; z0 + ct0).
+ Nếu (1) có vô số nghiệm thì (d) thuộc (α).

