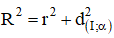Cho mặt cầu(S) có phương trình (x – 3)2 + (y + 2)2 + (z – 1)2 = 100

Toán lớp 12 Ôn tập chương 3 Hình học 12

Bài 5 (trang 92 SGK Hình học 12): Cho mặt cầu(S) có phương trình (x – 3)² + (y + 2)² + (z – 1)² = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0. Mp(α) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).

Lời giải:

Kiến thức áp dụng

+ Phương trình mặt cầu tâm I(a ; b ; c), bán kính R là :

(S) : (x – a)² + (y – b)² + (z – c)² = R².

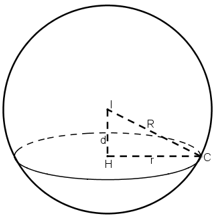
+ Mặt phẳng (α) cắt mặt cầu (S) tâm I, bán kính R có thiết diện là một đường tròn bán kính r, ta luôn có: