Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số trang 46 sgk Giải tích 12

Toán lớp 12 Bài ôn tập chương I

Bài 9 (trang 46 SGK Giải tích 12): a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:

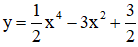
b) Viết phương tình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình f"(x) = 0.

c) Biện luận theo tham số m số nghiệm của phương trình: x⁴ - 6x² + 3 = m.

Lời giải:

a) Khảo sát hàm số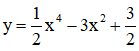

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

f'(x) = 2x³ - 6x = 2x(x² - 3)

f'(x) = 0 ⇔ 2x(x² - 3) = 0 ⇔ x = 0; x = ±√3

+ Giới hạn tại vô cực:

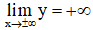
+ Bảng biến thiên:

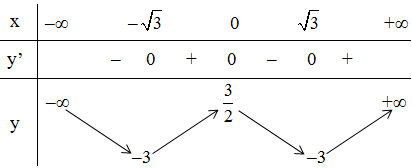
Kết luận: Hàm số đồng biến trên (-√3; 0) và (√3; +∞).

Hàm số nghịch biến trên (-∞; -√3) và (0; √3).

Hàm số đạt cực đại tại x = 0, y_CĐ =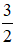

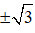
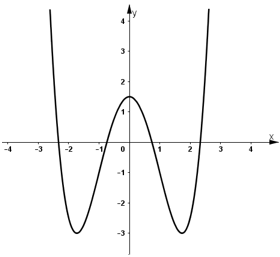
Hàm số đạt cực tiểu tại x = ; y_CT = -3.

- Đồ thị:

+ Đồ thị hàm số nhận trục tung là trục đối xứng.

+ Đồ thị cắt trục tung tại (0; 1,5).

b) Ta có: f"(x) = 6x² - 6 = 6(x² - 1)

f"(x) = 0 ⇔ 6(x² - 1) ⇔ x = ±1 ⇒ y = -1

Phương trình tiếp tuyến của (C) tại (-1; -1) là:

y = f'(-1)(x + 1) - 1 ⇒ y = 4x + 3

Phương trình tiếp tuyến của (C) tại (1; -1) là:

y = f'(1)(x - 1) - 1 ⇒ y = -4x + 3

c) Ta có: x⁴ - 6x² + 3 = m

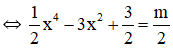
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.

Từ đồ thị (C) nhận thấy :

+ m/2 < - 3 ⇔ m < -6

⇒ đường thẳng (d) không cắt đồ thị (C)

⇒ Phương trình vô nghiệm.

+ m/2 = -3 ⇔ m = -6

⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu

⇒ Phương trình có 2 nghiệm.

+ -3 < m/2 < 3/2 ⇔ -6 < m < 3

⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt

⇒ Phương trình có 4 nghiệm.

+ m/2 = 3/2 ⇔ m = 3

⇒ đường thẳng (d) cắt (C) tại ba điểm

⇒ phương trình có 3 nghiệm.

+ m/2 > 3/2 ⇔ m > 3

⇒ đường thẳng (d) cắt (C) tại hai điểm

⇒ phương trình có hai nghiệm phân biệt.

Vậy:

+) m < - 6 thì phương trình vô nghiệm.

+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.

+) m = 3 thì PT có 3 nghiệm.

+) – 6 < m < 3 thì PT có 4 nghiệm.