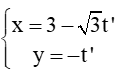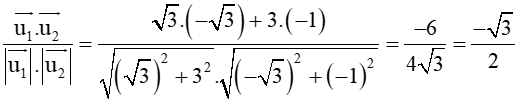Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆1 x=2+(căn3)t, y=-1+3t và ∆2 x=3-(căn3)t', y=-t'

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng và :

Giải sách bài tập Toán 10 Bài tập cuối chương 7

Bài 75 trang 98 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng 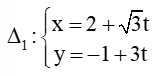và $Δ_{2}$ :

Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰;

B. 45⁰;

C. 90⁰;

D. 60⁰.

Lời giải:

Ta thấy vectơ chỉ phương của $Δ_{1}$ là: $\vec{u_{1}}$ =( $\sqrt{3}$ ;3)

Vectơ chỉ phương của $Δ_{2}$ là: $\vec{u_{2}}$ =(- $\sqrt{3}$ ;-1)

Ta có: cos( $\vec{u_{1}}$ , $\vec{u_{2}}$ )

= Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆1 x=2+(căn3)t, y=-1+3t và ∆2 x=3-(căn3)t', y=-t'

Suy ra ( $\vec{u_{1}}$ , $\vec{u_{2}}$ ) = 150^o

Suy ra góc giữa 2 đường thẳng chính là góc nhọn giữa 2 vectơ chỉ phương của 2 đường thẳng đó.

Do đó ( $Δ_{1}$ , $Δ_{2}$ )=180^o-( $\vec{u_{1}}$ , $\vec{u_{2}}$ )=30^o

Vậy chọn đáp án A.