Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 1; - 2), đường trung tuyến kẻ từ B

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 1; - 2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y – 5 = 0. Tìm tọa độ của hai điểm B và C.

Giải sách bài tập Toán 10 Bài tập cuối chương 7

Bài 83 trang 99 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 1; - 2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y – 5 = 0. Tìm tọa độ của hai điểm B và C.

Lời giải:

Gọi M là trung điểm của AC, K là hình chiếu của C lên AB.

Do CK vuông góc với AB nên AB có dạng: 3x – y + c = 0.

Thay A(-1; -2) vào phương trình trên ta có: 3. (-1) – (-2) + c = 0 ⇒ c = 1.

Phương trình đường thẳng AB: 3x – y + 1 = 0.

B là giao của AB và BM nên tọa độ của B là nghiệm của hệ:

Suy ra B(1; 4)

Do C thuộc CK nên C(5 – 3t; t)

M là trung điểm AC nên M$\left(\frac{4-3t}{2};\frac{t-2}{2}\right)$

M thuộc BM nên thay tọa độ M vào phương trình BM ta có:

5.$\frac{4-3t}{2}$+$\frac{t-2}{2}$-9=0$\iff$t=0

⇔ 20 – 15t + t – 2 – 18 = 0

⇔ – 14t = 0

⇔ t = 0

Suy ra C(5; 0).
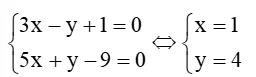
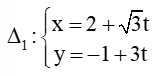