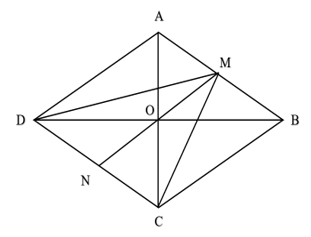
Cho hình thoi ABCD và M là trung điểm cạnh AB, N là trung điểm cạnh CD SBT Toán 10 Tập 1

Haylamdo biên soạn và sưu tầm lời giải Bài 1 trang 94 SBT Toán 10 Tập 1 trong Bài 2: Tổng và hiệu của hai vectơ. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Giải sách bài tập Toán 10 Bài 2: Tổng và hiệu của hai vectơ

Bài 1 trang 94 SBT Toán 10 Tập 1: Cho hình thoi ABCD và M là trung điểm cạnh AB, N là trung điểm cạnh CD. Chứng minh rằng: $\overrightarrow{\text{MA}}$ + $\overrightarrow{\text{MC}}$ = $\overrightarrow{\text{MB}}$ + $\overrightarrow{\text{MD}}$ = $\overrightarrow{\text{MN}}$.

Lời giải:

Gọi O là tâm hình thoi. O là trung điểm của AC và BD ( tính chất hình thoi).

⇒ $\overrightarrow{\text{OA}}$ + $\overrightarrow{\text{OC}}$ = $\overrightarrow{0}$ và $\overrightarrow{\text{OB}}$ + $\overrightarrow{\text{OD}}$ = $\overrightarrow{0}$.

Ta có:

$\overrightarrow{\text{MA}}$ + $\overrightarrow{\text{MC}}$ = $\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OA}}$ + $\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OC}}$ = 2$\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OA}}$ + $\overrightarrow{\text{OC}}$ = 2$\overrightarrow{\text{MO}}$ = $\overrightarrow{\text{MN}}$.

$\overrightarrow{\text{MB}}$ + $\overrightarrow{\text{MD}}$ = $\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OB}}$ + $\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OD}}$ = 2$\overrightarrow{\text{MO}}$ + $\overrightarrow{\text{OB}}$ + $\overrightarrow{\text{OD}}$ = 2$\overrightarrow{\text{MO}}$ = $\overrightarrow{\text{MN}}$.

Vậy $\overrightarrow{\text{MA}}$ + $\overrightarrow{\text{MC}}$ = $\overrightarrow{\text{MB}}$ + $\overrightarrow{\text{MD}}$ = $\overrightarrow{\text{MN}}$.