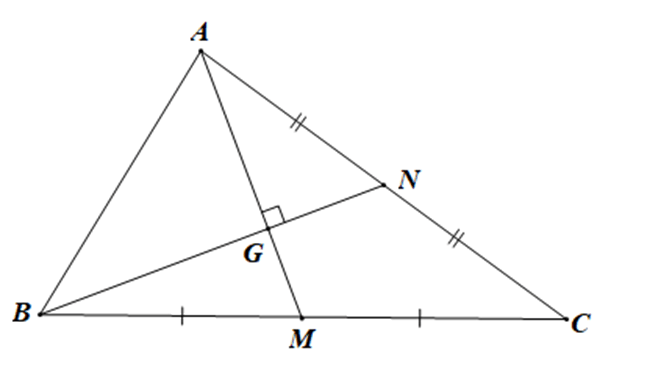
Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc

Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc.

Sách bài tập Toán 10 Kết nối tri thức Bài 6: Hệ thức lượng trong tam giác

Bài 3.14 trang 39 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có hai trung tuyến kẻ từ A và B vuông góc.

Chứng minh rằng:

a) a² + b² = 5c²;

b) cotC= 2 (cot A + cot B).

Lời giải:

a)

Gọi M, N lần lượt là trung điểm của các cạnh BC, AC.

Gọi G là trọng tâm của tam giác ABC.

Khi đó $AG=\frac{2}{3}AM$ và $BG=\frac{2}{3}BN.$

Áp dụng định lí Pythagore cho tam giác ABG vuông tại G (do AM ⊥ BN) có:

c² = AB² = AG² + BG²

$=\frac{4}{9}.A{M}^2+\frac{4}{9}.B{N}^2$

Mà AM, BN là hai đường trung tuyến kẻ từ A và B của tam giác ABC.

Do đó theo công thức tính độ dài đường trung tuyến của tam giác ta có:

$A{M}^2=m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}$ và $B{N}^2=m_b^2=\frac{a^2+c^2}{2}-\frac{b^2}{4}.$

Suy ra c² = $\frac{4}{9}.\left(\frac{b^2+c^2}{2}-\frac{a^2}{4}\right)+\frac{4}{9}.\left(\frac{a^2+c^2}{2}-\frac{b^2}{4}\right)$

$=\frac{4}{9}.\left(\frac{b^2+c^2}{2}-\frac{a^2}{4}+\frac{a^2+c^2}{2}-\frac{b^2}{4}\right)$

$=\frac{4}{9}.\left(\frac{a^2+b^2}{4}+c^2\right)$

$\Rightarrow$ c² $=\frac{4}{9}.\left(\frac{a^2+b^2}{4}+c^2\right)$

$\Rightarrow$ 9c² = a² + b² + 4c²

$\Rightarrow$ 5c² = a² + b².

b) Theo chứng minh phần a), Bài 3.13 ta có:

$\cot C=\frac{a^2+b^2-c^2}{4S}$

Mà 5c² = a² + b² (chứng minh phần a))

Do đó $\cot C=\frac{5c^2-c^2}{4S}=\frac{4c^2}{4S}=\frac{c^2}{S}$ (1)

Mặt khác:

$\cot A+\cot B=\frac{b^2+c^2-a^2}{4S}+\frac{a^2+c^2-b^2}{4S}$

$\Rightarrow$ cotA + cotB $=\frac{2c^2}{4S}=\frac{c^2}{2S}$

$\Rightarrow$ 2(cotA + cotB) $=\frac{c^2}{S}$ (2)

Từ (1) và (2) ta có: cotC = 2(cotA + cotB) = $\frac{c^2}{S}.$

Vậy cotC = 2(cotA + cotB).