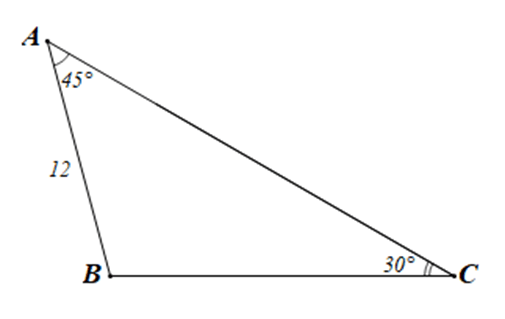
Cho tam giác ABC có góc A = 45 độ

Cho tam giác ABC có

Sách bài tập Toán 10 Kết nối tri thức Bài 6: Hệ thức lượng trong tam giác

Bài 3.7 trang 38 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có $\hat{A}=45°,\hat{C}=30°$ và c = 12.

a) Tính độ dài các cạnh còn lại của tam giác.

b) Tính độ dài bán kính đường tròn ngoại tiếp của tam giác.

c) Tính diện tích của tam giác.

d) Tính độ dài các đường cao của tam giác.

Lời giải:

Xét DABC có $\hat{A}+\hat{B}+\hat{C}=180°$

$\Rightarrow \hat{B}=180°-\hat{A}-\hat{C}=180°-45°-30°=105°.$

Áp dụng định lí sin ta có: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Suy ra:

$+$ $a=\frac{c}{\sin C}.\sin A=\frac{12}{\sin 30°}.\sin 45°$

$\Rightarrow a=\frac{12}{\frac{1}{2}}.\frac{\sqrt{2}}{2}=12\sqrt{2};$

$+$ $b=\frac{c}{\sin C}.\sin B=\frac{12}{\sin 30°}.\sin 105°$

$\Rightarrow b=\frac{12}{\frac{1}{2}}.\frac{\sqrt{6}+\sqrt{2}}{4}=6\sqrt{6}+6\sqrt{2}.$

Vậy $a=12\sqrt{2};b=6\sqrt{6}+6\sqrt{2}.$

b) Theo định lí sin ta có $\frac{c}{\sin C}=2R$

$\Rightarrow R=\frac{c}{2\sin C}=\frac{12}{2.\sin 30°}=12.$

Vậy bán kính đường tròn ngoại tiếp tam giác ABC bằng 12.

c) Áp dụng công thức diện tích tam giác ta có:

$S=\frac{1}{2}.bc\sin A=\frac{1}{2}.\left(6\sqrt{6}+6\sqrt{2}\right)\mathrm{.12.}\sin 45°$

$=6.\left(6\sqrt{6}+6\sqrt{2}\right).\frac{\sqrt{2}}{2}=36\sqrt{3}+36.$

Vậy diện tích tam giác ABC bằng $36\sqrt{3}+36.$

d) Áp dụng công thức diện tích tam giác ta có:

$S=\frac{1}{2}a{h}_a=\frac{1}{2}b{h}_b=\frac{1}{2}c{h}_c$

Do đó:

$+$ $h_a=\frac{2S}{a}=\frac{2.\left(36\sqrt{3}+36\right)}{12\sqrt{2}}=3\sqrt{6}+3\sqrt{2};$

$+$ $h_b=\frac{2S}{b}=\frac{2.\left(36\sqrt{3}+36\right)}{6\sqrt{6}+6\sqrt{2}}=6\sqrt{2};$

$+$ $h_c=\frac{2S}{c}=\frac{2.\left(36\sqrt{3}+36\right)}{12}=6\sqrt{3}+6.$

Vậy độ dài các đường cao h_a, h_b, h_c của tam giác ABC lần lượt là $h_a=3\sqrt{6}+3\sqrt{2};$ $h_b=6\sqrt{2};$ $h_c=6\sqrt{3}+6.$