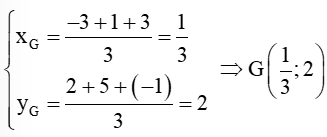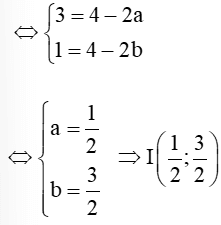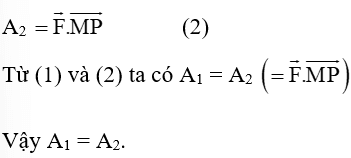Giải SBT Toán 10 trang 66 Tập 1 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 66 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 66.

Giải SBT Toán 10 trang 66 Tập 1 Kết nối tri thức

Bài 4.36 trang 66 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 2), B(1; 5) và C(3; −1).

a) Tìm toạ độ của điểm C thuộc trục hoành sao cho C cách đều A và B.

b) Tìm toạ độ của điểm D thuộc trục tung sao cho vectơ $\overrightarrow{DA}+\overrightarrow{DB}$ có độ dài ngắn nhất.

Lời giải:

a) Vì C cách đều A và B nên CA = CB

$\iff$ AC² = BC²

Giả sử C(x; 0) là điểm thuộc trục hoành

Với A(1; 1); B(7; 5) và C(x; 0) ta có:

• $\overrightarrow{AC}=\left(x-1;-1\right)$ $\Rightarrow$ AC² = (x – 1)² + (–1)²

$\Rightarrow$ AC² = x² – 2x + 2

• $\overrightarrow{BC}=\left(x-7;-5\right)$ $\Rightarrow$ BC² = (x – 7)² + (–5)²

$\Rightarrow$ BC² = x² – 14x + 74

Do đó AC² = BC²

$\iff$ x² – 2x + 2 = x² – 14x + 74

$\iff$ 12x = 72

$\iff$ x = 6

Vậy C(6; 0).

b) Gọi M là trung điểm của AB.

Khi đó $\overrightarrow{DA}+\overrightarrow{DB}=2\overrightarrow{DM}$

Do đó để vectơ $\overrightarrow{DA}+\overrightarrow{DB}$ có độ dài ngắn nhất thì vectơ $2\overrightarrow{DM}$ có độ dài ngắn nhất

$\iff$ DM có độ dài ngắn nhất

Hay DM² nhỏ nhất.

Giả sử D(0; y) là điểm thuộc trục tung

Với A(1; 1); B(7; 5) và D(0; y) ta có:

$\Rightarrow$ M(4; 3)

$\Rightarrow \overrightarrow{DM}=\left(4;3-y\right)$

$\Rightarrow$ DM² = 4² + (3 – y)²

Hay DM² = (y – 3)² + 16

Vì (y – 3)² ≥ 0 với mọi y

Nên (y – 3)² + 16 ≥ 16 với mọi y

Hay DM² ≥ 16 với mọi y

Dấu “=” xảy ra khi và chỉ khi y – 3 = 0 Û y = 3.

Do đó DM đạt giá trị nhỏ nhất khi D(0; 3)

Vậy D(0; 3) thì vectơ $\overrightarrow{DA}+\overrightarrow{DB}$ có độ dài ngắn nhất.

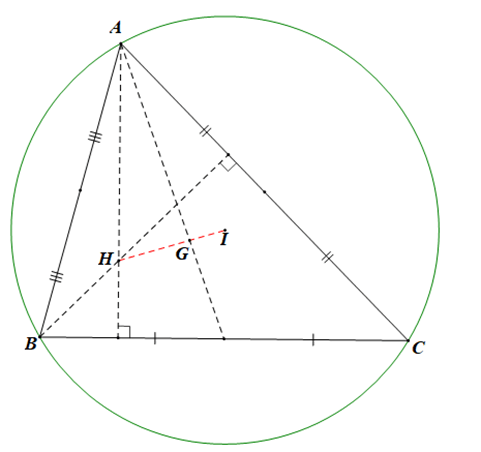
Bài 4.37 trang 66 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 2), B(1; 5) và C(3; −1).

a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm G của tam giác ấy.

b) Tìm toạ độ trực tâm H của tam giác ABC.

c) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tìm toạ độ của I.

Lời giải:

a) Với A(–3; 2), B(1; 5) và C(3; −1) ta có:

$\overrightarrow{AB}=\left(4;3\right)$ và $\overrightarrow{AC}=\left(6;-3\right)$

Vì $\frac{4}{6}=\frac{2}{3}\ne \frac{3}{-3}=-1$ nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ không cùng phương

Do đó ba điểm A, B, C không thẳng hàng

Vậy A, B, C là ba đỉnh của một tam giác.

Vì G là trọng tâm của tam giác ABC nên ta có:

Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{1}{3};2\right)$ .

b) Vì H là trực tâm của tam giác ABC nên AH ⊥ BC và BH ⊥ AC

Hay $\overrightarrow{AH}.\overrightarrow{BC}=0$ và $\overrightarrow{BH}.\overrightarrow{AC}=0$

Giả sử H(x; y) là tọa độ trực tâm tam giác ABC

Với A(–3; 2), B(1; 5), C(3; −1) và H(x; y) ta có:

• $\overrightarrow{AH}=\left(x+3;y-2\right)$ và $\overrightarrow{BC}=\left(2;-6\right)$

$\Rightarrow \overrightarrow{AH}.\overrightarrow{BC}=\left(x+3\right).2+\left(y-2\right).\left(-6\right)=0$

$\Rightarrow$ 2x – 6y = –18

$\Rightarrow$ x – 3y = –9 (1)

• $\overrightarrow{BH}=\left(x-1;y-5\right)$ và $\overrightarrow{AC}=\left(6;-3\right)$

$\Rightarrow \overrightarrow{BH}.\overrightarrow{AC}=\left(x-1\right).6+\left(y-5\right).\left(-3\right)=0$

$\Rightarrow$ 6x – 3y = –9 (2)

Trừ vế theo vế (2) cho (1) ta có:

5x = 0 $\Rightarrow$ x = 0

$\Rightarrow$ y = 3

$\Rightarrow$ H(0; 3)

Vậy tọa độ trực tâm của tam giác ABC là H(0; 3)

c) Theo kết quả phần a) của Bài 4.15, trang 54, Sách Bài tập, Toán 10, tập một ta có:

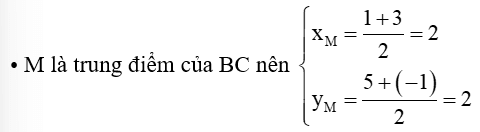
$\overrightarrow{AH}=2\overrightarrow{IM}$ với M là trung điểm của BC.

Giả sử I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC

Với A(–3; 2), B(1; 5), C(3; −1), H(0; 3) và I(a; b) ta có:

• $\overrightarrow{AH}=\left(3;1\right)$

$\Rightarrow$ M(2; 2)

$\Rightarrow \overrightarrow{IM}=\left(2-a;2-b\right)$

$\Rightarrow 2\overrightarrow{IM}=\left(4-2a;4-2b\right)$

Ta có $\overrightarrow{AH}=2\overrightarrow{IM}$

Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là $I\left(\frac{1}{2};\frac{3}{2}\right).$

Bài 4.38 trang 66 sách bài tập Toán lớp 10 Tập 1: Cho ba điểm M, N, P. Nếu một lực $\overrightarrow{F}$ không đổi tác động lên một chất điểm trong suốt quá trình chuyển động của chất điểm, thì các công sinh bởi lực $\overrightarrow{F}$ trong hai trường hợp sau có mối quan hệ gì với nhau?

a) Chất điểm chuyển động theo đường gấp khúc từ M đến N rồi tiếp tục từ N đến P.

b) Chất điểm chuyển động thẳng từ M đến P.

Lời giải:

a) Do lực $\overrightarrow{F}$ không đổi tác động lên một chất điểm trong suốt quá trình chuyển động của chất điểm nên công sinh bởi lực $\overrightarrow{F}$ khi chất điểm chuyển động theo đường gấp khúc từ M đến N rồi tiếp tục từ N đến P là:

A₁ = $\overrightarrow{F}.\overrightarrow{MN}+\overrightarrow{F}.\overrightarrow{NP}$

A₁$=\overrightarrow{F}.\left(\overrightarrow{MN}+\overrightarrow{NP}\right)$

A₁ $=\overrightarrow{F}.\overrightarrow{MP}$ (1)

b) Do lực $\overrightarrow{F}$ không đổi tác động lên một chất điểm trong suốt quá trình chuyển động của chất điểm nên công sinh bởi lực $\overrightarrow{F}$ khi chất điểm chuyển động thẳng từ M đến P là:

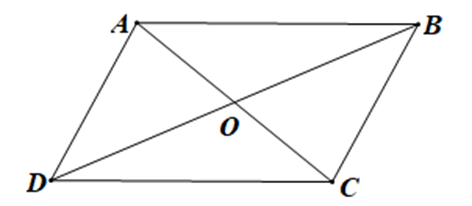
Bài 4.39 trang 66 sách bài tập Toán lớp 10 Tập 1: Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A, B, C, D và O. Số các vectơ khác vectơ - không và cùng phương với $\overrightarrow{AC}$ là:

A. 6;

B. 3;

C. 4;

D. 2.

Lời giải:

Đáp án đúng là: A

Các vectơ khác vectơ - không và cùng phương với $\overrightarrow{AC}$ là: $\overrightarrow{AC},\overrightarrow{CA},\overrightarrow{AO},\overrightarrow{OA},\overrightarrow{OC},\overrightarrow{CO}.$

Vậy có 6 vectơ khác vectơ - không và cùng phương với $\overrightarrow{AC}.$

Vậy ta chọn phương án A.

Bài 4.40 trang 66 sách bài tập Toán lớp 10 Tập 1: Cho đoạn thẳng AC và B là một điểm nằm giữa A, C. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?

A. Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CB}$ cùng hướng;

B. Hai vectơ $\overrightarrow{CA}$ và $\overrightarrow{BC}$ cùng hướng;

C. Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng;

D. Hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{BA}$ cùng hướng.

Lời giải:

Đáp án đúng là: C

Vì B nằm giữa A và C nên ta có:

• $\overrightarrow{AB}$ và $\overrightarrow{CB}$ ngược hướng. Do đó phương án A sai.

• $\overrightarrow{CA}$ và $\overrightarrow{BC}$ ngược hướng. Do đó phương án B sai.

• $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng. Do đó phương án C đúng.

• $\overrightarrow{AC}$ và $\overrightarrow{BA}$ ngược hướng. Do đó phương án D sai.

Vậy ta chọn phương án C.

Lời giải Sách bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 65 Tập 1
• Giải SBT Toán 10 trang 67 Tập 1
• Giải SBT Toán 10 trang 68 Tập 1
• Giải SBT Toán 10 trang 69 Tập 1
• Giải SBT Toán 10 trang 70 Tập 1