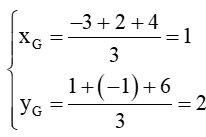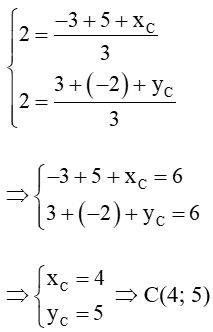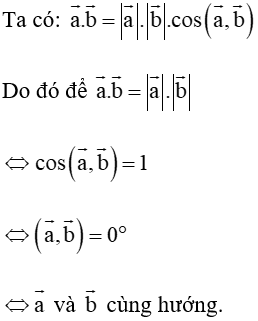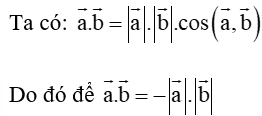Giải SBT Toán 10 trang 68 Tập 1 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 68 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 68.

Giải SBT Toán 10 trang 68 Tập 1 Kết nối tri thức

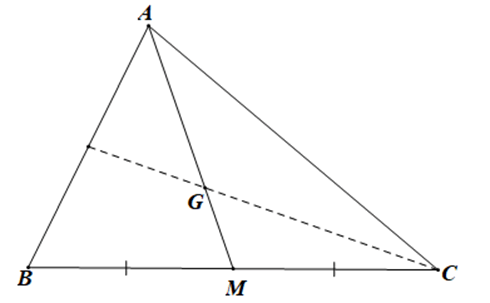
Bài 4.47 trang 68 sách bài tập Toán lớp 10 Tập 1: Gọi G là trọng tâm của tam giác ABC và M là trung điểm cạnh BC. Khẳng định nào sau đây là một khẳng định đúng?

A. $\overrightarrow{GA}=2\overrightarrow{GM};$

B. $\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG};$

C. $\overrightarrow{AM}=3\overrightarrow{MG};$

D. $3\overrightarrow{GA}=2\overrightarrow{AM}.$

Lời giải:

Đáp án đúng là: B

• Xét phương án A:

Vì G là trọng tâm của tam giác ABC nên AG = 2GM và G nằm giữa A, M.

Khi đó $\overrightarrow{GA},$ $\overrightarrow{GM}$ là hai vectơ ngược hướng

Nên $\overrightarrow{GA}=-2\overrightarrow{GM}$

Do đó phương án A là sai.

• Xét phương án B:

Vì M là trung điểm của BC nên $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$

Mà G là trọng tâm của tam giác ABC nên AG = $\frac{2}{3}$ AM

Hai vectơ $\overrightarrow{AG}$ và $\overrightarrow{AM}$ cùng hướng nên $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}$

$\Rightarrow 2\overrightarrow{AM}=3\overrightarrow{AG}$

Khi đó $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}=3\overrightarrow{AG}.$

Do đó phương án B là đúng.

• Xét phương án C:

Vì G là trọng tâm của tam giác ABC nên AM = 3MG và G nằm giữa A, M.

Khi đó $\overrightarrow{AM},$ $\overrightarrow{MG}$ là hai vectơ ngược hướng

Nên $\overrightarrow{AM}=-3\overrightarrow{MG}$

Do đó phương án C là sai.

• Xét phương án D:

Ta có $2\overrightarrow{AM}=3\overrightarrow{AG}$ (chứng minh khi xét phương án B)

Do đó phương án D là sai.

Vậy ta chọn phương án B.

Bài 4.48 trang 68 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 1), B(2; −1), C(4; 6). Trọng tâm G của tam giác ABC có toạ độ là

A. (1; 2);

B. (2; 1);

C. (1; –2);

D. (–2; 1).

Lời giải:

Đáp án đúng là: A

G là trọng tâm của tam giác ABC nên ta có:

$\Rightarrow$ G(1; 2)

Vậy ta chọn phương án A.

Bài 4.49 trang 68 sách bài tập Toán lớp 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 3), B(5; −2) và G(2; 2). Toạ độ của điểm C sao cho G là trọng tâm tam giác ABC là

A. (5; 4);

B. (4; 5);

C. (4; 3);

D. (3; 5).

Lời giải:

Đáp án đúng là: B

Vì G là trọng tâm của tam giác ABC nên ta có:

Vậy ta chọn phương án B.

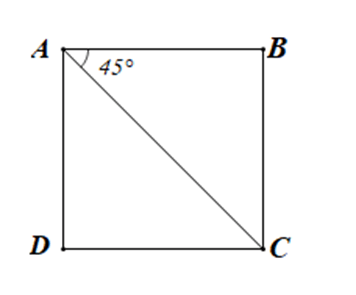
Bài 4.50 trang 68 sách bài tập Toán lớp 10 Tập 1: Cho hình vuông ABCD với độ dài cạnh bằng a. Tích vô hướng $\overrightarrow{AB}.\overrightarrow{AC}$ bằng:

A. a²$\sqrt{2};$

B. $\frac{a^2}{\sqrt{2}};$

C. a²;

D. $\frac{a^2}{2}.$

Lời giải:

Đáp án đúng là: C

Vì ABCD là hình vuông nên $∆$ABC vuông cân tại B

Do đó:

• $\widehat{BAC}=45°$

• AC = $\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$ (theo định lí Pythagore)

Ta có: $\overrightarrow{AB}.\overrightarrow{AC}$ = AB.AC.cos$\widehat{BAC}$

= a.a.$\sqrt{2}$.cos45°

= a.a$\sqrt{2}$ .$\frac{\sqrt{2}}{2}$

= a².

Do đó $\overrightarrow{AB}.\overrightarrow{AC}$= a².

Vậy ta chọn phương án C.

Bài 4.51 trang 68 sách bài tập Toán lớp 10 Tập 1: Cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ cùng khác $\overrightarrow{0}.$

A. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương;

B. $\overrightarrow{a}$ và $\overrightarrow{b}$ ngược hướng;

C. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng;

D. $\overrightarrow{a}\perp \overrightarrow{b.}$

Lời giải:

Đáp án đúng là: C

Vậy ta chọn phương án C.

Bài 4.52 trang 68 sách bài tập Toán lớp 10 Tập 1: Cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ cùng khác $\overrightarrow{0}.$

A. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương;

B. $\overrightarrow{a}$ và $\overrightarrow{b}$ ngược hướng;

C. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng;

D. $\overrightarrow{a}\perp \overrightarrow{b.}$

Lời giải:

Đáp án đúng là: B

$\iff cos\left(\overrightarrow{a},\overrightarrow{b}\right)=-1$

$\iff \left(\overrightarrow{a},\overrightarrow{b}\right)=180°$

$\iff \overrightarrow{a}$ và $\overrightarrow{b}$ ngược hướng.

Vậy ta chọn phương án B.

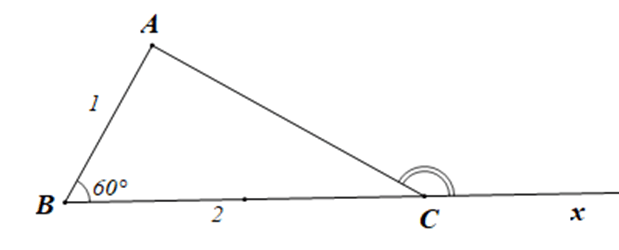
Bài 4.53 trang 68 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 1, BC = 2 và $\widehat{ABC}=60°.$ Tích vô hướng $\overrightarrow{BC}.\overrightarrow{CA}$ bằng

A. $\sqrt{3};$

B. $-\sqrt{3};$

C. 3;

D. –3.

Lời giải:

Đáp án đúng là: D

Ta có: $\overrightarrow{BC}.\overrightarrow{CA}$= BC.CA.cos$\left(\overrightarrow{BC},\overrightarrow{CA}\right)$

Kéo dài tia BC ta được tia Cx

Khi đó: $\left(\overrightarrow{BC},\overrightarrow{CA}\right)=\widehat{ACx}$

Tam giác ABC có AB = 1, BC = 2

Nên AB = $\frac{1}{2}$ BC

Lại có $\widehat{ABC}=60°.$

Do đó $∆$ABC vuông tại A.

Suy ra:

• AC = $\sqrt{B{C}^2-A{B}^2}=\sqrt{2^2-1^2}=\sqrt{3}$

• $\widehat{ACB}=90°-\widehat{ABC}=90°-60°=30°$

Mà $\widehat{ACx}=180°-\widehat{ACB}$ (do hai góc $\widehat{ACx}$ và $\widehat{ACB}$ kề bù)

$\Rightarrow \widehat{ACx}=180°-30°=150°$

Do đó $\overrightarrow{BC}.\overrightarrow{CA}$ = BC.CA.cos$\widehat{ACx}$

= 2.$\sqrt{3}$.cos150°

= 2.$\sqrt{3}.\frac{-\sqrt{3}}{2}$

= –3.

Vậy ta chọn phương án D.

Lời giải Sách bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 66 Tập 1
• Giải SBT Toán 10 trang 67 Tập 1
• Giải SBT Toán 10 trang 69 Tập 1
• Giải SBT Toán 10 trang 70 Tập 1
• Giải SBT Toán 10 trang 71 Tập 1