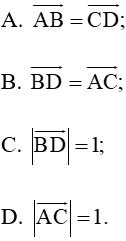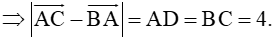Giải SBT Toán 10 trang 67 Tập 1 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 67 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 67.

Giải SBT Toán 10 trang 67 Tập 1 Kết nối tri thức

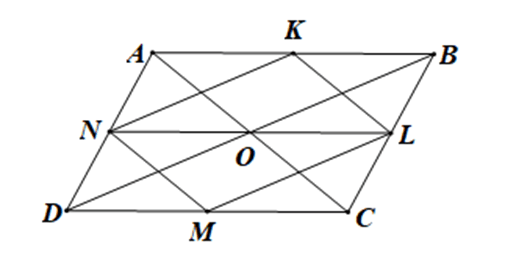
Bài 4.41 trang 67 sách bài tập Toán lớp 10 Tập 1: Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lấy từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ $\overrightarrow{AK}?$

A. 2;

B. 6;

C. 4;

D. 8.

Lời giải:

Đáp án đúng là: C

Vì ABCD là hình bình hành nên AB // CD và AB = CD.

Lại có K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA

Nên AK = KB = DM = MC và NL // AB // CD

Do đó ABLN là hình bình hành (do AB // NL và AN // BL)

Suy ra AB = NL = CD

Mà O là tâm hình bình hành nên O là trung điểm của AC và BD

Do đó đường trung bình NL đi qua O

Và NO = OL = $\frac{1}{2}NL=\frac{1}{2}AB=\frac{1}{2}CD$

Suy ra AK = KB = NO = OL = DM = MC.

Khi đó các vectơ bằng vectơ $\overrightarrow{AK}$ là: $\overrightarrow{KB},\overrightarrow{OL},\overrightarrow{DM},\overrightarrow{MC}.$

Vậy có 4 vectơ bằng vectơ $\overrightarrow{AK}.$

Ta chọn phương án C.

Bài 4.42 trang 67 sách bài tập Toán lớp 10 Tập 1: >Cho hình thoi ABCD có độ dài các cạnh bằng 1 và $\widehat{DAB}=120°.$ Khẳng định nào sau đây là đúng?

Lời giải:

Đáp án đúng là: D

• Xét phương án A:

Vì ABCD là hình thoi nên AB // CD suy ra $\overrightarrow{AB}=\overrightarrow{DC}.$

Do đó phương án A là sai.

• Xét phương án B:

Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.

Khi đó $\overrightarrow{BD}\perp \overrightarrow{AC}$ nên $\overrightarrow{BD}\ne \overrightarrow{AC}.$

Do đó phương án B là sai.

• Xét phương án C:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = AB = 1.

Xét $∆$ABD có AB = AD = 1 và $\widehat{DAB}=120°,$ áp dụng định lí cosin ta có:

BD² = AD² + AB² – 2.AD.AB.cos$\widehat{DAB}$

$\Rightarrow$ BD² = 1² + 1² – 2.1.1.cos120°

$\Rightarrow$ BD² = 3

$\Rightarrow$ BD = $\sqrt{3}$

Do đó phương án C là sai.

• Xét phương án D:

Vì ABCD là hình thoi có cạnh bằng 1 nên AD = CD = 1 .

Mặt khác $\widehat{DAB}=120°$ nên $\widehat{ADC}=180°-\widehat{DAB}=180°-120°=60°$

Tam giác ADC có AD = DC nên là tam giác cân lại có $\widehat{ADC}=60°$

Suy ra DADC là tam giác đều

$\Rightarrow$ AC = AD = CD = 1.

Do đó phương án D là đúng.

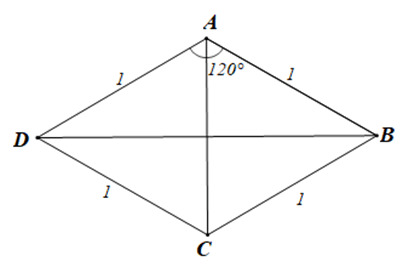
Bài 4.43 trang 67 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài của vectơ $\overrightarrow{AG}$ bằng

A. $\sqrt{3};$

B. $\frac{3\sqrt{3}}{2};$

C. $\frac{\sqrt{3}}{2};$

D. $2\sqrt{3}.$

Lời giải:

Đáp án đúng là: A

Tam giác ABC đều có cạnh bằng 3 nên AB = AC = 3 và $\widehat{BAC}=60°.$

Gọi M là trung điểm của BC.

Khi đó ta có: $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$

$\Rightarrow {\left(\overrightarrow{AB}+\overrightarrow{AC}\right)}^2={\left(2\overrightarrow{AM}\right)}^2$

$\Rightarrow A{B}^2+2.\overrightarrow{AB}.\overrightarrow{AC}+A{C}^2=4A{M}^2$

$\Rightarrow A{B}^2+2.AB.AC.c\text{os}\widehat{BAC}+A{C}^2=4A{M}^2$

$\Rightarrow$ 3² + 2.3.3.cos60° + 3² = 4.AM²

$\Rightarrow$ 4.AM² = 27

$\Rightarrow$ AM² = $\frac{27}{4}$

$\Rightarrow$ AM = $\sqrt{\frac{27}{4}}=\frac{3\sqrt{3}}{2}$

Vì G là trọng tâm tam giác ABC nên AG = $\frac{2}{3}$ AM

$\Rightarrow$ AG = $\frac{2}{3}.\frac{3\sqrt{3}}{2}=\sqrt{3}.$

Vậy ta chọn phương án A.

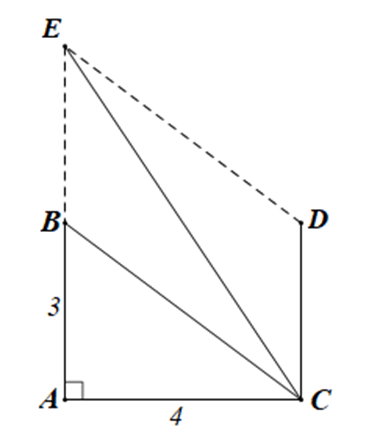
Bài 4.44 trang 67 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC vuông tại A và AB = 3, AC = 4. Độ dài của vectơ $\overrightarrow{CB}+\overrightarrow{AB}$ bằng

A. $\sqrt{13};$

B. $2\sqrt{13};$

C. 4;

D. 2.

Lời giải:

Đáp án đúng là: B

Gọi D là điểm thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$

Khi đó CD // AB và CD = AB (1)

Ta có: $\overrightarrow{CB}+\overrightarrow{AB}=\overrightarrow{CB}+\overrightarrow{CD}$

Gọi E là điểm thỏa mãn BCDE là hình bình hành.

Khi đó CD // BE và CD = BE (2)

Từ (1) và (2) ta có: AB ≡ BE và AB = BE

Do đó B là trung điểm của AE

$\Rightarrow$ AE = 2AB = 2.3 = 6.

Xét tam giác ACE vuông tại A, theo định lí Pythagore ta có:

CE² = AC² + AE² = 4² + 6² = 52

$\Rightarrow$ CE = $\sqrt{52}=2\sqrt{13}.$

Vì ABCD là hình bình hành nên $\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CE}$ (quy tắc hình bình hành)

Vậy ta chọn phương án B.

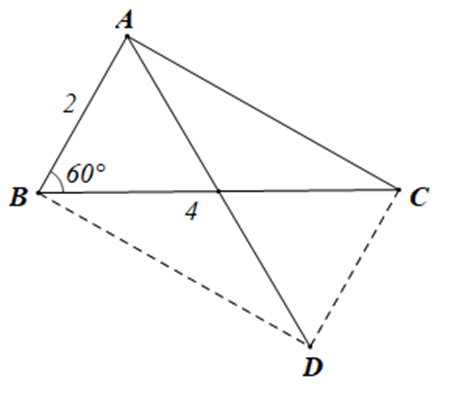
Bài 4.45 trang 67 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 2, BC = 4 và $\widehat{ABC}=60°.$ Độ dài của vectơ $\overrightarrow{AC}-\overrightarrow{BA}$ bằng

A. 2;

B. 4;

C. $\sqrt{19};$

D. $\frac{\sqrt{19}}{2}.$

Lời giải:

Đáp án đúng là: C

Xét DABC có AB = 2, BC = 4 và $\widehat{ABC}=60°.$

Khi đó tam giác ABC là tam giác vuông tại A.

$\Rightarrow \widehat{BAC}=90°.$

Ta có: $\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AC}+\overrightarrow{AB}$

Gọi D là điểm thỏa mãn ABDC là hình bình hành

Khi đó $\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AD}$

Hình bình hành ABDC có $\widehat{BAC}=90°$ nên là hình chữ nhật.

Do đó AD = BC (hai đường chéo bằng nhau)

Vậy ta chọn phương án C.

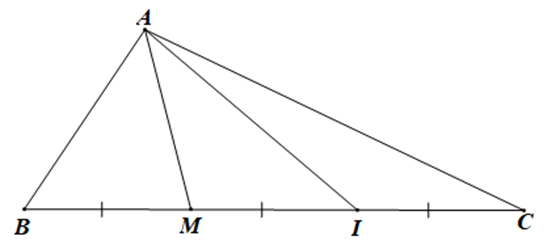
Bài 4.46 trang 67 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC và điểm I sao cho $\overrightarrow{IB}+2\overrightarrow{IC}=\overrightarrow{0}.$ Khẳng định nào sau đây là một khẳng định đúng?

A. $\overrightarrow{AI}=2\overrightarrow{AC}-\overrightarrow{AB};$

B. $\overrightarrow{AI}=\overrightarrow{AB}-2\overrightarrow{AC};$

C. $\overrightarrow{AI}=\frac{\overrightarrow{AB}-2\overrightarrow{AC}}{-3};$

D. $\overrightarrow{AI}=\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{3}.$

Lời giải:

Đáp án đúng là: D

Ta có: $\overrightarrow{IB}+2\overrightarrow{IC}=\overrightarrow{0}\Rightarrow \overrightarrow{IB}=-2\overrightarrow{IC}$

Khi đó $\overrightarrow{IB}$ và $\overrightarrow{IC}$ là hai vectơ cùng phương, ngược hướng và IB = 2IC.

Khi đó điểm I nằm giữa hai điểm B và C sao cho IB = 2IC.

Gọi M là trung điểm của BI.

Khi đó M là trung điểm của BI, I là trung điểm của MC.

Vì I là trung điểm của MC nên ta có:

$2\overrightarrow{AI}=\overrightarrow{AM}+\overrightarrow{AC}$ (1)

Vì M là trung điểm của BI nên ta có:

$2\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AI}$

$\Rightarrow \overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AI}$ (2)

Thay (2) vào (1) ta được:

$2\overrightarrow{AI}=\overrightarrow{AM}+\overrightarrow{AC}$

$\Rightarrow 2\overrightarrow{AI}=\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AI}\right)+\overrightarrow{AC}$

$\Rightarrow 2\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AI}+\overrightarrow{AC}$

$\Rightarrow 2\overrightarrow{AI}-\frac{1}{2}\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}$

$\Rightarrow \frac{3}{2}\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}$

$\Rightarrow \overrightarrow{AI}=\frac{2}{3}.\left(\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AC}\right)$

$\Rightarrow \overrightarrow{AI}=\frac{\overrightarrow{AB}+2\overrightarrow{AC}}{3}$

Vậy ta chọn phương án D.

Lời giải Sách bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 66 Tập 1
• Giải SBT Toán 10 trang 68 Tập 1
• Giải SBT Toán 10 trang 69 Tập 1
• Giải SBT Toán 10 trang 70 Tập 1
• Giải SBT Toán 10 trang 71 Tập 1