Giải SBT Toán 10 trang 70 Tập 1 Kết nối tri thức

❮ Bài trước Bài sau ❯

Với Giải SBT Toán 10 trang 70 Tập 1 trong Bài 11: Tích vô hướng của hai vectơ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 70.

Giải SBT Toán 10 trang 70 Tập 1 Kết nối tri thức

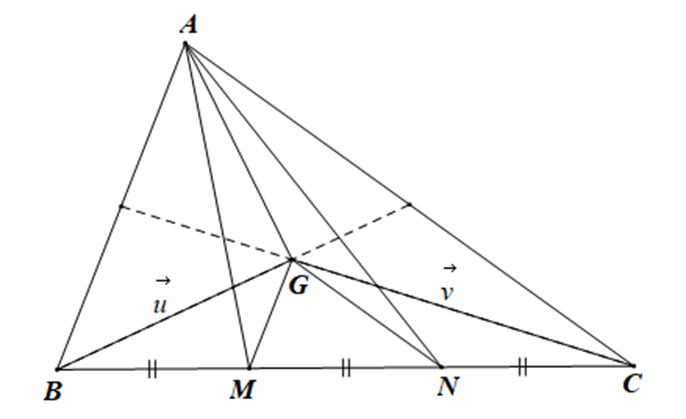
Bài 4.60 trang 70 sách bài tập Toán lớp 10 Tập 1: Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.

a) Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm.

b) Gọi G là trọng tâm của tam giác ABC. Đặt $\vec{G B} = \vec{u}$ và $\vec{G C} = \vec{v} .$ Hãy biểu thị các vectơ sau qua hai vectơ $\vec{u}$ và $\vec{v} :$ $\vec{G A}, \vec{G M}, \vec{G N} .$

Lời giải:

a) Giả sử G, G' lần lượt là trọng tâm của DABC, DAMN.

Sử dụng kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có: $\vec{AA} + \vec{B M} + \vec{C N} = 3 \vec{G G^{'}}$

$\Rightarrow \vec{B M} + \vec{C N} = 3 \vec{G G^{'}}$

Mặt khác: M, N lần lượt lấy theo thứ tự trên cạnh BC sao cho BM = MN = NC nên ta có: $\vec{B M} = \vec{M N} = \vec{N C}$

$\Rightarrow \vec{B M} = - \vec{C N} \Rightarrow \vec{B M} + \vec{C N} = \vec{0}$

$\Rightarrow \vec{B M} + \vec{C N} = 3 \vec{G G^{'}} = \vec{0}$

Suy ra điểm G và G' trùng nhau.

Do đó hai tam giác ABC và AMN có cùng trọng tâm.

b) • Vì G là trọng tâm của tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

$\Rightarrow \vec{G A} = - \vec{G B} - \vec{G C}$

$\Rightarrow \vec{G A} = - \vec{u} - \vec{v}$

• Từ BM = MN = NC suy ra $\vec{M C} = - 2 \vec{M B}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm G ta có:

$\vec{G C} - (- 2) \vec{G B} = (1 - (- 2)) \vec{G M}$

$\Rightarrow 3 \vec{G M} = \vec{G C} + 2 \vec{G B}$

$\Rightarrow \vec{G M} = \frac{2}{3} \vec{G B} + \frac{1}{3} \vec{G C} = \frac{2}{3} \vec{u} + \frac{1}{3} \vec{v}$

Tương tự ta cũng có: $\vec{G N} = \frac{1}{3} \vec{u} + \frac{2}{3} \vec{v}$

Bài 4.61 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 5 và $\hat{C A B} = 60 ° .$

a) Tính tích vô hướng $\vec{A B} . \vec{A C}, \vec{A B} . \vec{B C} .$

b) Lấy các điểm M, N thoả mãn $2 \vec{A M} + 3 \vec{M C} = \vec{0}$ và $\vec{N B} + x \vec{N C} = \vec{0}$ (x ≠ –1). Xác định x sao cho AN vuông góc với BM.

Lời giải:

a) Ta có:

• $\vec{A B} . \vec{A C}$ = AB. AC.cos $\hat{B A C}$ = 4.5.cos60° = 10.

• $\vec{A B} . \vec{B C} = \vec{A B} . (\vec{A C} - \vec{A B})$

= $\vec{A B} . \vec{A C}$ – AB²

= 10 – 4²

= 10 – 16

= –6

Vậy $\vec{A B} . \vec{A C} = 10,$ $\vec{A B} . \vec{B C} = - 6.$

b) Ta có

• $2 \vec{A M} + 3 \vec{M C} = \vec{0}$

$\Rightarrow 2 (\vec{B M} - \vec{B A}) + 3 (\vec{B C} - \vec{B M}) = \vec{0}$

$\Rightarrow 2 \vec{B M} - 2 \vec{B A} + 3 \vec{B C} - 3 \vec{B M} = \vec{0}$

$\Rightarrow \vec{B M} = - 2 \vec{B A} + 3 \vec{B C}$

$= 2 \vec{A B} + 3 (\vec{A C} - \vec{A B})$

$= 2 \vec{A B} + 3 \vec{A C} - 3 \vec{A B}$

$= 3 \vec{A C} - \vec{A B}$

• $\vec{N B} + x \vec{N C} = \vec{0}$

$\Rightarrow \vec{A B} - \vec{A N} + x (\vec{A C} - \vec{A N}) = \vec{0}$

$\Rightarrow \vec{A B} - \vec{A N} + x \vec{A C} - x \vec{A N} = \vec{0}$

$\Rightarrow \vec{A B} + x \vec{A C} - (1 + x) \vec{A N} = \vec{0}$

$\Rightarrow (1 + x) \vec{A N} = \vec{A B} + x \vec{A C}$

Do đó:

$(1 + x) \vec{A N} . \vec{B M} = (\vec{A B} + x \vec{A C}) . (3 \vec{A C} - \vec{A B})$

$= 3 \vec{A B} . \vec{A C} - A B^{2} + 3 x A C^{2} - x \vec{A B} . \vec{A C}$

$= (3 - x) \vec{A B} . \vec{A C} - A B^{2} + 3 x A C^{2}$

= (3 – x).10 – 4² + 3x.5²

= 30 – 10x – 16 + 75x

= 65x + 14

Để AN ⊥ BM thì $\vec{A N} . \vec{B M} = 0$

$\Leftrightarrow (1 + x) \vec{A N} . \vec{B M} = 0$ (với x ≠ –1)

$\Leftrightarrow$ 65x + 14 = 0

$\Leftrightarrow$ x = $- \frac{14}{65}$

Vậy với x = $- \frac{14}{65}$ thì AN ⊥ BM.

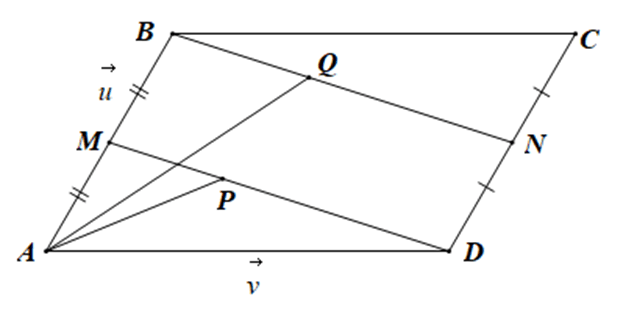
Bài 4.62 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM và Q thuộc đoạn BN sao cho DP = 2PM, BQ = xQN. Đặt $\vec{A B} = \vec{u}$ và $\vec{A D} = \vec{v} .$

a) Hãy biểu thị các vectơ $\vec{A P}, \vec{A Q}$ qua hai vectơ $\vec{u}$ và $\vec{v} .$

b) Tìm x đề A, P, Q thằng hàng.

Lời giải:

• Vì P thuộc đoạn DM sao cho DP = 2PM

Nên $\vec{P D} = - 2 \vec{P M}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

$\vec{A D} - (- 2) \vec{A M} = (1 - (- 2)) \vec{A P}$

$\Rightarrow 3 \vec{A P} = \vec{A D} + 3 \vec{A M}$

$\Rightarrow \vec{A P} = \frac{1}{3} \vec{A D} + \vec{A M}$

$\Rightarrow \vec{A P} = \frac{1}{3} \vec{A D} + \frac{1}{2} \vec{A B}$ (vì M là trung điểm của AB)

$\Rightarrow \vec{A P} = \frac{1}{3} \vec{v} + \frac{1}{2} \vec{u}$

• Vì Q thuộc đoạn BN sao cho BQ = xQN

$\Rightarrow \vec{Q B} = - x \vec{Q N}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

$\vec{A B} - (- x) \vec{A N} = (1 - (- x)) \vec{A Q}$

$\Rightarrow (1 + x) \vec{A Q} = \vec{A B} + x \vec{A N}$

$= \vec{A B} + x (\vec{A D} + \vec{D N})$

$= \vec{A B} + x \vec{A D} + x \vec{D N}$

$= \vec{A B} + x \vec{A D} + x . \frac{1}{2} \vec{D C}$ (vì N là trung điểm của CD)

$= \vec{A B} + x \vec{A D} + \frac{1}{2} x \vec{A B}$ (vì $\vec{D C} = \vec{A B}$ )

$= (1 + \frac{1}{2} x) \vec{A B} + x \vec{A D}$

$\Rightarrow (1 + x) \vec{A Q} = \frac{x + 2}{2} \vec{u} + x \vec{v}$

$\Rightarrow \vec{A Q} = \frac{x + 2}{2 (x + 1)} \vec{u} + \frac{x}{x + 1} \vec{v}$ (do x ≠ −1)

b) Với $\vec{A P} = \frac{1}{3} \vec{v} + \frac{1}{2} \vec{u}$ và $\vec{A Q} = \frac{x + 2}{2 (x + 1)} \vec{u} + \frac{x}{x + 1} \vec{v}$

Để A, P, Q thẳng hàng thì hai vectơ $\vec{A P}$ và $\vec{A Q}$ cùng phương

$\Leftrightarrow \frac{\frac{x + 2}{2 (x + 1)}}{\frac{1}{3}} = \frac{\frac{x}{x + 1}}{\frac{1}{3}}$ $\Leftrightarrow \frac{x + 2}{2 (x + 1)} = \frac{x}{x + 1}$

$\Leftrightarrow \frac{x + 2}{2 (x + 1)} = \frac{x}{x + 1}$

$\Rightarrow$ x + 2 = 2x

$\Rightarrow$ x = 2 (thỏa mãn x ≠ –1)

Vậy x = 2 thì ba điểm A, P, Q thẳng hàng.

Bài 4.63 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC với trọng tâm G. Lấy điểm A', B' sao cho $\vec{A A^{'}} = 2 \vec{B C},$ $\vec{B B^{'}} = 2 \vec{C A} .$ Gọi G' là trọng tâm của tam giác A'B'C. Chứng minh rằng GG' song song với AB.

Lời giải:

Theo kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có:

$\vec{A A'} + \vec{B B^{'}} + \vec{C C} = 3 \vec{G G^{'}}$

$\Rightarrow \vec{A A'} + \vec{B B^{'}} = 3 \vec{G G^{'}}$

$\Rightarrow 2 \vec{B C} + 2 \vec{C A} = 3 \vec{G G^{'}}$

$\Rightarrow 2 (\vec{B C} + \vec{C A}) = 3 \vec{G G^{'}}$

$\Rightarrow 2 \vec{B A} = 3 \vec{G G^{'}}$

$\Rightarrow \vec{G G^{'}} = \frac{2}{3} \vec{B A}$

Do đó $\vec{G G^{'}}$ cùng phương với $\vec{B A}$

Suy ra GG' // AB (do G và G' không nằm trên đường thẳng AB)

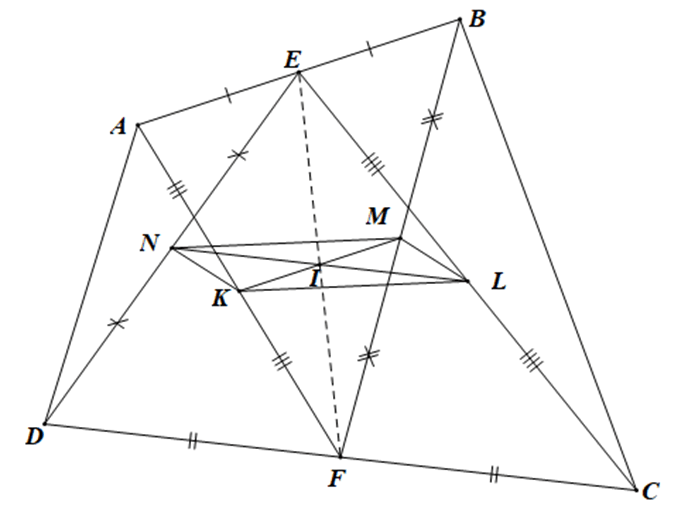
Bài 4.64 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD. Gọi K, L, M, N lần lượt là trung điểm của AF, CE, BF, DE.

a) Chứng minh rằng tứ giác KLMN là một hình bình hành.

b) Gọi I là giao điểm của KM, LN. Chứng minh rằng E, I, F thẳng hàng.

Lời giải:

• Vì E là trung điểm của AB nên $\vec{A E} = \vec{E B}$

F là trung điểm của CD nên $\vec{F C} = \vec{D F} .$

• Vì K là trung điểm của AF, L là trung điểm của CE, theo kết quả của Bài tập 4.12, trang 58, Toán 10, Tập một, ta có:

$2 \vec{K L} = \vec{A E} + \vec{F C} = \vec{E B} + \vec{D F}$

Tương tự:

M là trung điểm của BF, N là trung điểm của DE, nên ta có:

$\vec{E B} + \vec{D F} = 2 \vec{N M}$

Do đó $2 \vec{K L} = 2 \vec{N M}$

$\Rightarrow \vec{K L} = \vec{N M}$

$\Rightarrow$ KL = NM và KL // NM

$\Rightarrow$ KLMN là một hình bình hành.

b) Do KLMN là hình bình hành

Mà I là giao điểm của KM, LN nên I là trung điểm chung của KM, LN.

Khi đó ta có:

$2 \vec{E I} = \vec{E N} + \vec{E L} = \frac{1}{2} \vec{E D} + \frac{1}{2} \vec{E C}$

$= \frac{1}{2} (\vec{E D} + \vec{E C}) = \frac{1}{2} . \vec{E F}$ (do F là trung điểm của DC)

Do đó $2 \vec{E I} = \frac{1}{2} . \vec{E F}$

$\Rightarrow \vec{E I} = \frac{1}{4} . \vec{E F}$

Suy ra hai vectơ $\vec{E I}$ và $\vec{E F}$ cùng phương

Do đó E, I, F thẳng hàng.

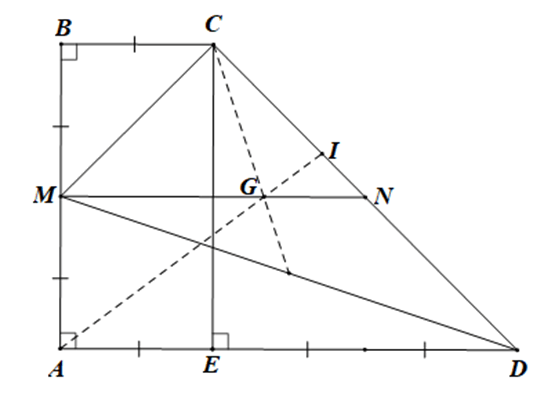
Bài 4.65 trang 70 sách bài tập Toán lớp 10 Tập 1: Cho hình thang vuông ABCD có $\hat{D A B} = \hat{A B C} = 90 °,$ BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.

a) Hãy biểu thị các vectơ $\vec{C M}, \vec{C M}$ theo hai vectơ $\vec{A B}$ và $\vec{A D} .$

b) Gọi N là trung điểm CD, G là trọng tâm tam giác MCD, và I là điểm thuộc cạnh CD sao cho 9IC = 5ID. Chứng minh rằng A, G, I thẳng hàng.

c) Tính độ dài các đoạn thẳng AI và BI.

Lời giải:

a) Vì M là trung điểm của AB nên $\vec{B M} = \frac{1}{2} \vec{B A} = - \frac{1}{2} \vec{A B}$

Gọi E là hình chiếu của C trên AD. Khi đó $\hat{C E A} = 90 °$

Tứ giác ABCE có $\hat{D A B} = \hat{A B C} = \hat{C E A} = 90 °$ nên là hình chữ nhật

$\Rightarrow$ EA = CB = 1

Mà AD = 3 do đó AE = $\frac{1}{3}$ AD

$\Rightarrow \vec{E A} = \frac{1}{3} \vec{D A} = - \frac{1}{3} \vec{A D}$

Mà $\vec{C B} = \vec{E A}$ (do ABCE là hình chữ nhật)

$\Rightarrow \vec{C B} = - \frac{1}{3} \vec{A D}$

$\Rightarrow \vec{C M} = \vec{C B} + \vec{B M} = - \frac{1}{3} \vec{A D} - \frac{1}{2} \vec{A B}$

• Ta có: $\vec{C D} = \vec{C E} + \vec{E D}$

Mà $\vec{C E} = \vec{B A}$ (do ABCE là hình chữ nhật)

Và $\vec{E D} = \frac{2}{3} \vec{A D}$

$\Rightarrow \vec{C D} = \vec{B A} + \frac{2}{3} \vec{A D} = - \vec{A B} + \frac{2}{3} \vec{A D}$

Vậy $\vec{C M} = - \frac{1}{3} \vec{A D} - \frac{1}{2} \vec{A B}$ và $\vec{C D} = - \vec{A B} + \frac{2}{3} \vec{A D} .$

b) Vì G là trọng tâm của tam giác MCD nên ta có:

$\vec{A M} + \vec{A C} + \vec{A D} = 3 \vec{A G}$

ABCD là hình chữ nhật nên cũng là hình bình hành

Do đó $\vec{A C} = \vec{A B} + \vec{A E}$

$\Rightarrow 3 \vec{A G} = \vec{A M} + (\vec{A B} + \vec{A E}) + \vec{A D}$

$= \frac{1}{2} \vec{A B} + \vec{A B} + \frac{1}{3} \vec{A D} + \vec{A D}$ (do $\vec{A E} = \frac{1}{3} \vec{A D}$ )

$= \frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D}$

Vì I thuộc cạnh CD nên hai vectơ $\vec{I C}$ và $\vec{I D}$ ngược hướng nhau

Lại có 9IC = 5ID nên $9 \vec{I C} = - 5 \vec{I D}$ hay $\vec{I C} = - \frac{5}{9} \vec{I D}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:

$\vec{A C} - (- \frac{5}{9}) \vec{A D} = (1 - (- \frac{5}{9})) \vec{A I}$

$\Rightarrow \vec{A C} + \frac{5}{9} \vec{A D} = (1 + \frac{5}{9}) \vec{A I}$

$\Rightarrow \vec{A C} + \frac{5}{9} \vec{A D} = \frac{14}{9} \vec{A I}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A C} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 (\vec{A B} + \vec{A E}) + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 9 \vec{A E} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 9. \frac{1}{3} \vec{A D} + 5 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D}$

$\Rightarrow 14 \vec{A I} = 6 (\frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D})$

$\Rightarrow 14 \vec{A I} = 6.3 \vec{A G}$ (do $3 \vec{A G} = \frac{3}{2} \vec{A B} + \frac{4}{3} \vec{A D}$ )

$\Rightarrow 14 \vec{A I} = 18 \vec{A G}$

$\Rightarrow \vec{A I} = \frac{9}{7} \vec{A G}$

Do đó hai vectơ $\vec{A I}$ và $\vec{A G}$ cùng phương

Suy ra ba điểm A, I, G thẳng hàng.

c) • Theo câu a ta có $14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D}$

$\Rightarrow {(14 \vec{A I})}^{2} = {(9 \vec{A B} + 8 \vec{A D})}^{2}$

$\Rightarrow 196 A I^{2} = 81 A B^{2} + 2. (9 \vec{A B}) . (8 \vec{A D}) + 64 A D^{2}$

Mà AB ⊥ AD nên $\vec{A B} . \vec{A D} = 0$

Do đó ta có: 196AI² = 81AB² + 64AD²

$\Rightarrow$ 196AI² = 81.2² + 64.3² = 900

$\Rightarrow$ AI² = $\frac{225}{49}$

$\Rightarrow$ AI = $\frac{15}{7} .$

• Ta có: $14 \vec{A I} = 9 \vec{A B} + 8 \vec{A D} \Rightarrow \vec{A I} = \frac{9}{14} \vec{A B} + \frac{4}{7} \vec{A D}$

$\Rightarrow$ $\vec{B I} = \vec{A I} - \vec{A B} = \frac{9}{14} \vec{A B} + \frac{4}{7} \vec{A D} - \vec{A B}$

$\Rightarrow \vec{B I} = - \frac{5}{14} \vec{A B} + \frac{4}{7} \vec{A D}$

$\Rightarrow {(\vec{B I})}^{2} = {(- \frac{5}{14} \vec{A B} + \frac{4}{7} \vec{A D})}^{2}$

$\Rightarrow B I^{2} = \frac{25}{196} A B^{2} - 2. \frac{5}{14} \vec{A B} . \frac{4}{7} \vec{A D} + \frac{16}{49} A D^{2}$

$\Rightarrow B I^{2} = \frac{25}{196} A B^{2} + \frac{16}{49} A D^{2}$ (do $\vec{A B} . \vec{A D} = 0$ )

$\Rightarrow B I^{2} = \frac{25}{196} {.2}^{2} + \frac{16}{49} {.3}^{2} = \frac{169}{49}$

$\Rightarrow$ BI = $\frac{13}{7} .$

Vậy AI = $\frac{15}{7}$ và BI = $\frac{13}{7} .$

Lời giải Sách bài tập Toán lớp 10 Bài 11: Tích vô hướng của hai vectơ Kết nối tri thức hay khác:

Xem thêm lời giải Sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

❮ Bài trước Bài sau ❯