Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC). Trong mặt phẳng (ABC), gọi H là hình chiếu của A trên BC
Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC). Trong mặt phẳng (ABC), gọi H là hình chiếu của A trên BC. Chứng minh rằng BC ⊥ A’H.
Giải sách bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 11 trang 94 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC). Trong mặt phẳng (ABC), gọi H là hình chiếu của A trên BC. Chứng minh rằng BC ⊥ A’H.
Lời giải:
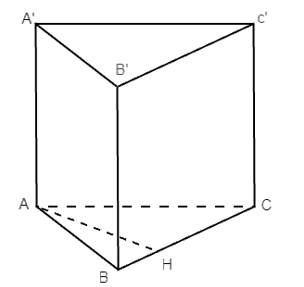
Do AA’ ⊥ (ABC) nên AA’ ⊥ BC.
Ta có: BC ⊥ AA’; BC ⊥ AH;
AA’ ∩ AH = A trong (A’AH).
Suy ra: BC ⊥ (A’AH).
Mà A’H ⊂ (A’AH) nên BC ⊥ A’H.
Lời giải SBT Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay khác:
Bài 14 trang 95 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi, AA’ ⊥ (ABCD). Chứng minh rằng:....
Bài 15 trang 95 SBT Toán 11 Tập 2: Cho hình chóp O.ABC và điểm H không thuộc các đường thẳng AB, BC, CA....
Bài 16 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC. ...
Bài 17 trang 95 SBT Toán 11 Tập 2: Cho tam giác ABC và các điểm M, N, P đôi một phân biệt thoả mãn MA = MB = MC, NA = NB = NC, PA = PB = PC....
Bài 18 trang 95 SBT Toán 11 Tập 2: Cho hình tứ diện đều ABCD. Chứng minh AB ⊥ CD....
Bài 19 trang 95 SBT Toán 11 Tập 2: Cho hình tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. ....
Bài 20 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA....
Bài 21 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD thoả mãn SA = SB = SC = SD. Chứng minh rằng tồn tại một đường tròn đi qua cả bốn đỉnh của tứ giác ABCD.....

