Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC
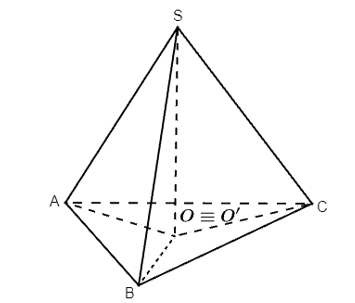
Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC. Chứng minh rằng SO ⊥ (ABC).
Giải sách bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 16 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABC thoả mãn SA = SB = SC. Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC. Chứng minh rằng SO ⊥ (ABC).
Lời giải:
Gọi O’ là hình chiếu của S trên (ABC). Khi đó, SO’ ⊥ (ABC).
Mà O’A, O’B, O’C đều nằm trên (ABC) nên SO’ ⊥ O’A, SO’ ⊥ O’B, SO’ ⊥ O’C.
Xét tam giác SO’A và tam giác SO’B có:
SA = SB (gt);
SO’ chung
Suy ra ∆SO’A = ∆SO’B (cạnh huyền – cạnh góc vuông)
Do đó: O’A = O’B (hai cạnh tương ứng)
Tương tự: ∆SO’A = ∆SO’C, suy ra O’A = O’C.
Từ đó ta có: O’A = O’B = O’C hay O’ là tâm đường tròn ngoại tiếp tam giác ABC.
Suy ra: O ≡ O’, mà SO’ ⊥ (ABC).
Vậy SO ⊥ (ABC).
Lời giải SBT Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay khác: