Cho tứ diện ABCD. Trên cạnh CD lấy hai điểm M và N khác nhau
Cho tứ diện ABCD. Trên cạnh CD lấy hai điểm M và N khác nhau. Chứng minh rằng các đường thẳng AM và BN không cắt nhau.
Giải SBT Toán 11 Cánh diều Bài tập cuối chương 4
Bài 55 trang 118 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Trên cạnh CD lấy hai điểm M và N khác nhau. Chứng minh rằng các đường thẳng AM và BN không cắt nhau.
Lời giải:
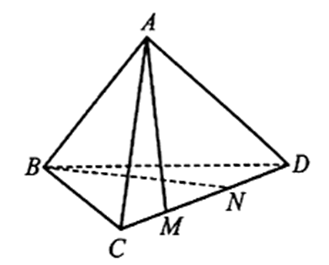
Giả sử hai đường thẳng AM và BN cắt nhau.
Khi đó, qua AM và BN có một mặt phẳng (P).
Do M, N thuộc (P) nên đường thẳng MN nằm trong (P) hay CD nằm trong (P).
Suy ra A, B, C, D cùng thuộc một mặt phẳng, mâu thuẫn với giả thiết.
Vậy AM và BN không cắt nhau.
Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 4 hay khác:
Bài 52 trang 117 SBT Toán 11 Tập 1: Cho bốn điểm A, B, C, D không cùng thuộc một mặt phẳng. Khẳng định nào sau đây là sai? ....
Bài 53 trang 117 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Trên cạnh SA lấy điểm M sao cho MA = 2MS ....
Bài 54 trang 118 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Trên cạnh BC lấy điểm M sao cho MB = 2MC. Mặt phẳng (P) đi qua M và song song với mặt phẳng (ABD) cắt cạnh AC tại N ....
Bài 56 trang 118 SBT Toán 11 Tập 1: Cho mặt phẳng (P), ba điểm A, B, C không thẳng hàng và không nằm trên (P) ....
Bài 57 trang 118 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh SD ....
Bài 58 trang 118 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC (P, Q không là trung điểm của CD, CB) ....
Bài 59 trang 118 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC ....
Bài 60 trang 118 SBT Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BC, B'C'. Chứng minh rằng AM // (A'NC) ....
Bài 61 trang 118 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, BC, CD ....
Bài 62 trang 118 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm của AD, B'C', DD' ....
Bài 63 trang 119 SBT Toán 11 Tập 1: Vẽ hình biểu diễn của một số đồ vật có dạng hình chóp, hình lăng trụ, ... trong lớp học ....

