Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC
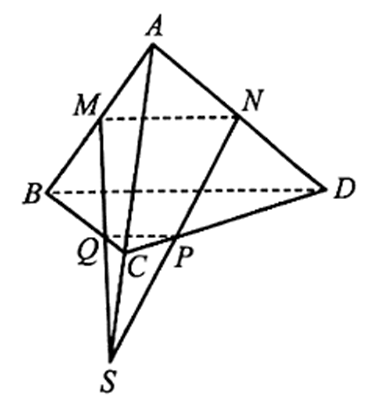
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC (P, Q không là trung điểm của CD, CB). Chứng minh rằng nếu M, N, P, Q cùng thuộc một mặt phẳng thì ba đường thẳng MQ, NP và AC cùng đi qua một điểm.
Giải SBT Toán 11 Cánh diều Bài tập cuối chương 4
Bài 58 trang 118 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD; P, Q lần lượt thuộc các cạnh CD, BC (P, Q không là trung điểm của CD, CB). Chứng minh rằng nếu M, N, P, Q cùng thuộc một mặt phẳng thì ba đường thẳng MQ, NP và AC cùng đi qua một điểm.
Lời giải:
Giả sử M, N, P, Q cùng thuộc một mặt phẳng.
Xét tam giác ABC, do Q không là trung điểm của BC nên đường thẳng MQ cắt đường thẳng AC tại điểm S.
Khi đó, S ∈ (MNPQ) và S ∈ (ACD). Do vậy S là một điểm chung của hai mặt phẳng (ACD) và (MNPQ). (1)
Do N ∈ AD nên N ∈ (ACD) và P ∈ CD nên P ∈ (ACD), suy ra NP ⊂ (ACD).
Mà NP ⊂ (MNPQ) nên NP là giao tuyến của hai mặt phẳng (ACD) và (MNPQ). (2)
Từ (1) và (2) suy ra S ∈ NP.
Vậy ba đường thẳng MQ, NP và AC cùng đi qua điểm S.
Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 4 hay khác: