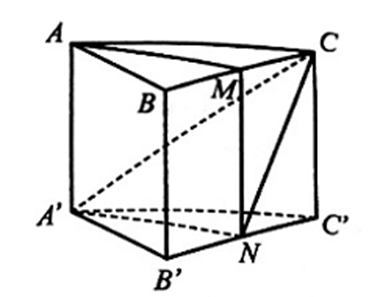
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BC, B'C'
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BC, B'C'. Chứng minh rằng AM // (A'NC).
Giải SBT Toán 11 Cánh diều Bài tập cuối chương 4
Bài 60 trang 118 SBT Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BC, B'C'. Chứng minh rằng AM // (A'NC).
Lời giải:
Vì M, N lần lượt là trung điểm của BC, B'C' nên MN là đường trung bình của hình thang BCC'B' (vì hình bình hành cũng là hình thang).
Suy ra MN // BB' và MN = BB'.
Mà AA' // BB' và AA' = BB' (do ABC.A'B'C' là hình lăng trụ).
Do đó, AA' // MN và AA' = MN nên AA'NM là hình bình hành.
Suy ra AM // A'N, mà A'N ⊂ (A'NC).
Vậy AM // (A'NC).
Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 4 hay khác: