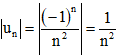Chứng minh rằng lim (-1)^n / n^2 = 0

Giải sách bài tập Toán 11 Bài 1: Giới hạn của dãy số

Bài 6 trang 68 SBT Toán 11 Tập 1: Chứng minh rằng $\lim \frac{{\left(-1\right)}^n}{n^2}=0$ .

Lời giải:

Xét dãy số (u_n) có $u_n=\frac{{\left(-1\right)}^n}{n^2}$.

Giả sử h là số dương bé tùy ý cho trước. Ta có:

Do đó, .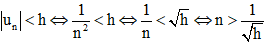

Vậy với các số tự nhiên n lớn hơn $\frac{1}{\sqrt{h}}$  thì |u­_n| < h.

Suy ra $\lim \frac{{\left(-1\right)}^n}{n^2}=0$ .

Lời giải Sách bài tập Toán lớp 11 Bài 1: Giới hạn của dãy số Cánh diều hay khác:

• Bài 1 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai? ....

• Bài 2 trang 68 SBT Toán 11 Tập 1: Cho limu_n = a, lim v_n = b. Phát biểu nào sau đây là sai? ....

• Bài 3 trang 68 SBT Toán 11 Tập 1: Nếu limu_n = C và limv_n = +∞ (hoặc limv_n = −∞) thì $\lim \frac{u_n}{v_n}$  bằng: ....

• Bài 4 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai? ....

• Bài 5 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng? ....

• Bài 7 trang 68 SBT Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với $u_n=3-\frac{4}{n+1}$ , $v_n=8-\frac{5}{3n^2+2}$ . Tính: ....

• Bài 8 trang 68 SBT Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 9 trang 69 SBT Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 10 trang 69 SBT Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (u­_n) với $u_1=\frac{5}{4},q=-\frac{1}{3}$ . ....

• Bài 11 trang 69 SBT Toán 11 Tập 1: Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm đất ....