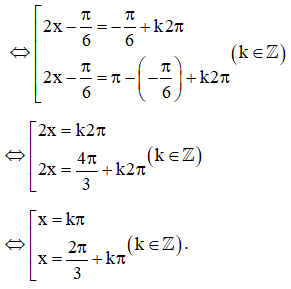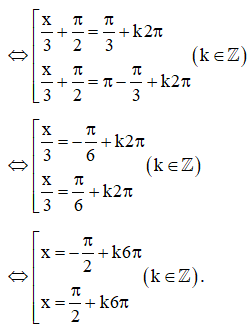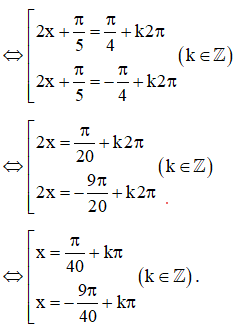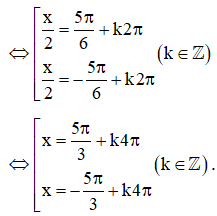Giải phương trình trang 32 SBT Toán 11

❮ Bài trước Bài sau ❯

Giải phương trình:

Giải sách bài tập Toán 11 Bài tập cuối chương 1

Bài 72 trang 32 SBT Toán 11 Tập 1: Giải phương trình:

a) $\sin (2 x - \frac{π}{6}) = - \frac{1}{2}$ ;

b) $\sin (\frac{x}{3} + \frac{π}{2}) = \frac{\sqrt{3}}{2}$ ;

c) $\cos (2 x + \frac{π}{5}) = \frac{\sqrt{2}}{2}$ ;

d) $2 \cos \frac{x}{2} + \sqrt{3} = 0$ ;

e) $\sqrt{3} \tan (2 x + \frac{π}{3}) - 1 = 0$ ;

g) cot(3x + π) = – 1.

Lời giải:

a) Do $\sin (- \frac{π}{6}) = - \frac{1}{2}$ nên $\sin (2 x - \frac{π}{6}) = - \frac{1}{2}$ $\Leftrightarrow \sin (2 x - \frac{π}{6}) = \sin (- \frac{π}{6})$

Giải phương trình trang 32 SBT Toán 11

b) Do $\sin \frac{π}{3} = \frac{\sqrt{3}}{2}$ nên $\sin (\frac{x}{3} + \frac{π}{2}) = \frac{\sqrt{3}}{2}$ $\Leftrightarrow \sin (\frac{x}{3} + \frac{π}{2}) = \sin \frac{π}{3}$

Giải phương trình trang 32 SBT Toán 11

c) Do $\cos \frac{π}{4} = \frac{\sqrt{2}}{2}$ nên $\cos (2 x + \frac{π}{5}) = \frac{\sqrt{2}}{2}$ $\Leftrightarrow \cos (2 x + \frac{π}{5}) = \cos \frac{π}{4}$

Giải phương trình trang 32 SBT Toán 11

d) $2 \cos \frac{x}{2} + \sqrt{3} = 0$

$\Leftrightarrow \cos \frac{x}{2} = - \frac{\sqrt{3}}{2}$

$\Leftrightarrow \cos \frac{x}{2} = \cos \frac{5 π}{6}$ (do $\cos \frac{5 π}{6} = - \frac{\sqrt{3}}{2}$ )

Giải phương trình trang 32 SBT Toán 11

e) $\sqrt{3} \tan (2 x + \frac{π}{3}) - 1 = 0$

$\Leftrightarrow \tan (2 x + \frac{π}{3}) = \frac{1}{\sqrt{3}}$

$\Leftrightarrow \tan (2 x + \frac{π}{3}) = \tan \frac{π}{6}$ (do $\tan \frac{π}{6} = \frac{1}{\sqrt{3}}$ )

$\Leftrightarrow 2 x + \frac{π}{3} = \frac{π}{6} + k π (k \in ℤ)$

$\Leftrightarrow 2 x = - \frac{π}{6} + k π (k \in ℤ)$

$\Leftrightarrow x = - \frac{π}{12} + k \frac{π}{2} (k \in ℤ)$ .

g) Do $\cot (- \frac{π}{4}) = - 1$ nên cot(3x + π) = – 1 $\Leftrightarrow \cot (3 x + π) = \cot (- \frac{π}{4})$

$\Leftrightarrow 3 x + π = - \frac{π}{4} + k π (k \in ℤ)$

$\Leftrightarrow 3 x = - \frac{5 π}{4} + k π (k \in ℤ)$

$\Leftrightarrow x = - \frac{5 π}{12} + k \frac{π}{3} (k \in ℤ)$ .

Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 1 Cánh diều hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯