Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC

❮ Bài trước Bài sau ❯

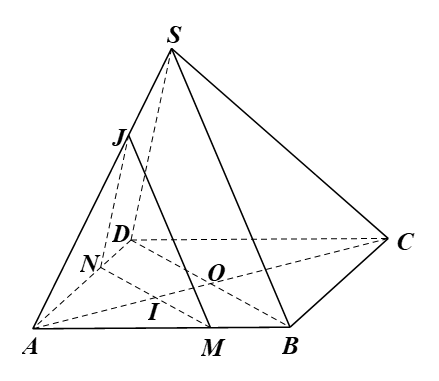
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 2a, BD = 2b; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < a), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD).

Giải sách bài tập Toán 11 Bài tập cuối chương 4 - Chân trời sáng tạo

Bài 5 trang 133 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 2a, BD = 2b; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < a), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD).

a) Xác định giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD.

b) Tính diện tích của hình tạo bởi các đoạn giao tuyến ở câu a theo a, b và x.

Lời giải:

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC

a) Trong mặt phẳng (ABCD), kẻ MN đi qua I và MN // BD (M ∈ AB, N ∈ AD).

Trong mặt phẳng (SAD), kẻ NJ // SD (J ∈ SA).

Trong mặt phẳng (SAB), nối JM.

Ta có MN // BD và BD ⊂ (SBD) nên MN // (SBD). Do đó mặt phẳng (P) chính là mặt phẳng (MNJ)

Khi đó, (P) ∩ (SAB) = JM; (P) ∩ (SAD) = JN; (P) ∩ (ABCD) = MN.

b) Các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD tạo thành tam giác MNJ.

Ta có ∆JMN ∽ ∆SBD nên ∆JMN là tam giác đều.

Ta có MN // BD, suy ra: $\frac{M N}{B D} = \frac{A I}{A O} = \frac{x}{a}$ => MN = $\frac{2 b x}{a}$

=> S_∆JMN = $\frac{1}{2} \cdot M N \cdot M J . \sin \hat{N M J}$ = $\frac{1}{2} M N^{2} \sin 60 °$ = $\frac{1}{2} \cdot {(\frac{2 b x}{a})}^{2} \cdot \frac{\sqrt{3}}{2}$ = $\frac{b^{2} x^{2} \sqrt{3}}{a^{2}}$ .

Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 4 hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯