Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD
Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP) là đường thẳng d. Khẳng định nào dưới đây đúng?
Giải sách bài tập Toán 11 Bài tập cuối chương 4 - Chân trời sáng tạo
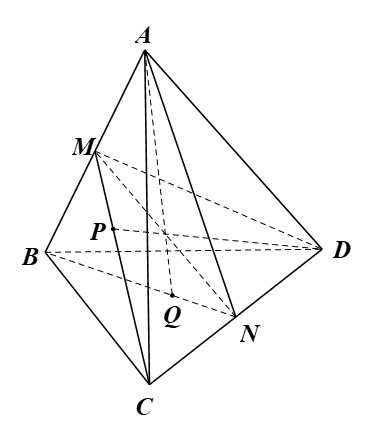
Câu 7 trang 132 SBT Toán 11 Tập 1: Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP) là đường thẳng d. Khẳng định nào dưới đây đúng?
A. d đi qua trung điểm hai cạnh AB và CD.
B. d đi qua trung điểm hai cạnh AB và AD.
C. d là đường thẳng PQ.
D. d là đường thẳng QA.
Lời giải:
Đáp án đúng là: A
Gọi M, N lần lượt là trung điểm của AB, CD.
Ta có M ∈ AB mà AB ⊂ (ABQ), nên M ∈ (ABQ) (1)
Khi đó đường trung tuyến CM đi qua trọng tâm P của của ∆ABC.
Do đó mặt phẳng (DCP) chính là mặt phẳng (DCM), nên M ∈ (DCP) (2)
Từ (1) và (2) suy ra M ∈ (ABQ) ∩ (DCP).
Tương tự ta cũng có N ∈ (ABQ) ∩ (DCP).
Suy ra (ABQ) ∩ (DCP) = MN.
Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 4 hay khác:
Câu 1 trang 132 SBT Toán 11 Tập 1: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất? ....
Câu 5 trang 132 SBT Toán 11 Tập 1: Trong không gian, hai đường thẳng không có điểm chung thì ....