Cho hình lăng trụ ABC.A'B'C' có A'B'C' và AA'C' là hai tam giác đều cạnh a

Cho hình lăng trụ ABC.A'B'C' có A'B'C' và AA'C' là hai tam giác đều cạnh a. Biết (ACC'A') (A'B'C'). Tính theo a thể tích khối lăng trụ ABC.A'B'C'.

Giải sách bài tập Toán 11 Bài 27: Thể tích - Kết nối tri thức

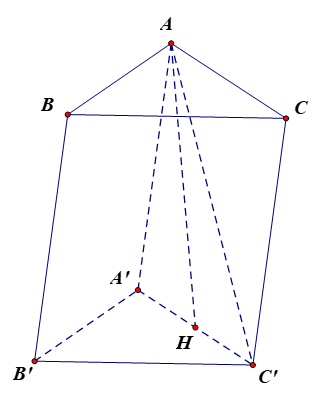
Bài 7.35 trang 41 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A'B'C' có A'B'C' và AA'C' là hai tam giác đều cạnh a. Biết (ACC'A') $\perp$ (A'B'C'). Tính theo a thể tích khối lăng trụ ABC.A'B'C'.

Lời giải:

Kẻ AH $\perp$ A'C' tại H mà (ACC'A') $\perp$ (A'B'C') và (ACC'A') $\cap$ (A'B'C') = A'C' nên

AH $\perp$ (A'B'C').

Tam giác A'B'C' là tam giác đều cạnh a nên $S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{a^2\sqrt{3}}{4}$.

Tam giác AA'C' là tam giác đều cạnh a, AH là đường cao nên AH = $\frac{a\sqrt{3}}{2}$.

Vậy $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}\cdot AH=\frac{a^2\sqrt{3}}{4}\cdot \frac{a\sqrt{3}}{2}=\frac{3a^3}{8}$.

Lời giải SBT Toán 11 Bài 27: Thể tích hay khác:

• Bài 7.33 trang 41 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC); AB = a, AC = a$\sqrt{2}$ và $\widehat{SBA}=60°$, $\widehat{BAC}=45°$ ....

• Bài 7.34 trang 41 SBT Toán 11 Tập 2: Cho khối chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60° ....

• Bài 7.36 trang 41 SBT Toán 11 Tập 2: Cho tứ diện OABC có OA = OB = OC = a và $\widehat{AOB}=90°$; $\widehat{BOC}=60°$; $\widehat{COA}=120°$ ....

• Bài 7.37 trang 41 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, biết SO $\perp$ (ABCD) ....

• Bài 7.38 trang 41 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC), SA = a và đáy ABC là tam giác vuông tại A, AB = a, AC = a$\sqrt{3}$. Kẻ AM vuông góc với SB tại M, AN vuông góc với SC tại N ....

• Bài 7.39 trang 41 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC) và $\widehat{BAC}=60°$, biết diện tích các tam giác ABC, SAB và SAC lần lượt là 3$\sqrt{3}$; 9; 12 ....

• Bài 7.40 trang 41 SBT Toán 11 Tập 2: Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh 1 m để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp ....