Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II

Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.

Giải SBT Toán 12 Cánh diều Bài 2: Công thức xác suất toàn phần. Công thức Bayes

Bài 16 trang 95 SBT Toán 12 Tập 2: Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.

Lời giải:

Xét các biến cố:

A: “Chọn được xạ thủ hạng I”;

B: “Viên đạn đó trúng mục tiêu”.

Khi đó, P(A) = $\frac{4}{10}$ = 0,4; P($\overline{A}$) = 1 – P(A) = 0,6.

             P(B | A) = 0,75; P(B | $\overline{A}$) = 0,6.

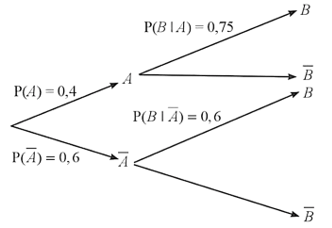
Sơ đồ hình cây biểu thị tình huống đã cho là:

Áp dụng công thức xác suất toàn phần, ta có:

P(B) = P(A) . P(B | A) + P($\overline{A}$) . P(B | $\overline{A}$) = 0,4 . 0,75 + 0,6 . 0,6 = 0,66.

Vậy xác suất để viên đạn đó trúng mục tiêu là 0,66.

Lời giải SBT Toán 12 Bài 2: Công thức xác suất toàn phần. Công thức Bayes hay khác:

• Bài 10 trang 94 SBT Toán 12 Tập 2: Nếu hai biến cố A, B thỏa mãn P(B) = 0,4; P(A | B) = 0,5; P(A |$\overline{B}$) = 0,3 thì P(A) bằng: ....

• Bài 11 trang 94 SBT Toán 12 Tập 2: Nếu hai biến cố A, B thỏa mãn P(A) = 0,3; P(B) = 0,6; P(A | B) = 0,4 thì P(B | A) bằng ....

• Bài 12 trang 94 SBT Toán 12 Tập 2: Một kho hàng có các thùng hàng với bề ngoài giống hệt nhau, trong đó có 24 thùng hàng loại I ....

• Bài 13 trang 95 SBT Toán 12 Tập 2: Trước khi đưa ra thị trường một sản phẩm, công ty phỏng vấn 800 khách hàng và được kết quả là 550 người nói sẽ mua ....

• Bài 14 trang 95 SBT Toán 12 Tập 2: Huy thực hiện liên tiếp hai thí nghiệm. Thí nghiệm thứ nhất có xác suất thành công là 0,6 ....

• Bài 15 trang 95 SBT Toán 12 Tập 2: Một xí nghiệp mỗi ngày sản xuất ra 1 600 sản phẩm, trong đó có 35 sản phẩm lỗi ....