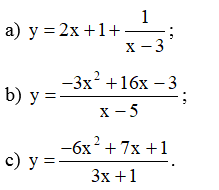Tìm các tiệm cận của đồ thị hàm số sau: y = 2x + 1 + 1/(x - 3)

Tìm các tiệm cận của đồ thị hàm số sau:

Giải SBT Toán 12 Chân trời sáng tạo Bài 3: Đường tiệm cận của đồ thị hàm số

Bài 3 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:

Lời giải:

a) $y = 2 x + 1 + \frac{1}{x - 3}$

Ta có: $\lim_{x \to 3^{+}} y = \lim_{x \to 3^{+}} (2 x + 1 + \frac{1}{x - 3}) = + \infty$ ; $\lim_{x \to 3^{-}} y = \lim_{x \to 3^{-}} (2 x + 1 + \frac{1}{x - 3}) = - \infty$ .

Do đó, đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to \pm \infty} [y - (2 x + 1)] = \lim_{x \to \pm \infty} \frac{1}{x - 3} = 0$ .

Do đó, đường thẳng y = 2x + 1laf tiệm cận xiên của đồ thị hàm số.

b) Ta có: $y = \frac{- 3 x^{2} + 16 x - 3}{x - 5}$ = −3x + 1 + $\frac{2}{x - 5}$ .

$\lim_{x \to 5^{+}} y = \lim_{x \to 5^{+}} (- 3 x + 1 + \frac{2}{x - 5}) = + \infty$ ; $\lim_{x \to 5^{-}} y = \lim_{x \to 5^{-}} (- 3 x + 1 + \frac{2}{x - 5}) = - \infty$ .

Do đó, đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to \pm \infty} [y - (- 3 x + 1)] = \lim_{x \to \pm \infty} \frac{2}{x - 5} = 0$ .

Do đó, đường thẳng y = −3x + 1 là tiệm cận xiên của đồ thị hàm số.

c) Ta có: $y = \frac{- 6 x^{2} + 7 x + 1}{3 x + 1}$ = −2x + 3 – $\frac{2}{3 x + 1}$

$\lim_{x \to - {\frac{1}{3}}^{+}} y = \lim_{x \to - {\frac{1}{3}}^{+}} (- 2 x + 3 - \frac{2}{3 x + 1}) = + \infty$ ; $\lim_{x \to - {\frac{1}{3}}^{-}} y = \lim_{x \to - {\frac{1}{3}}^{-}} (- 2 x + 3 - \frac{2}{3 x + 1}) = - \infty$ .

Do đó, đường thẳng x = $- \frac{1}{3}$ là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to \pm \infty} [y - (- 2 x + 3)] = \lim_{x \to \pm \infty} \frac{- 2}{3 x + 1} = 0$ .

Do đó, đường thẳng y = −2x + 3 là tiệm cận xiên của đồ thị hàm số.

Lời giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯