Lợi nhuận thu được P của một công ty khi dùng số tiền s chi cho quảng cáo được cho bởi công thức

Giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Bài 1.16 trang 15 SBT Toán 12 Tập 1: Lợi nhuận thu được P của một công ty khi dùng số tiền s chi cho quảng cáo được cho bởi công thức

P = P(s) = $- \frac{1}{10}$ s³ + 6s² + 400, s ≥ 0.

Ở đây các số được tính bằng đơn vị nghìn USD.

a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa.

b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?

Lời giải:

a) Ta có: P' = $- \frac{3}{10}$ s² + 12s

P' = 0 ⇔ $- \frac{3}{10}$ s² + 12s = 0 ⇔ s = 0 hoặc s = 40.

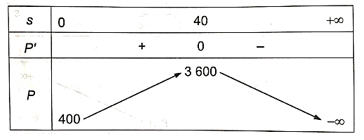
Ta có bảng biến thiên:

Lợi nhuận thu được P của một công ty khi dùng số tiền s chi cho quảng cáo được cho bởi công thức

Vậy để mang lại lợi nhuận tối đa, số tiền công ty phải chi cho quảng cáo là 40 nghìn USD.

b) Từ bảng biến thiên, suy ra:

Lợi nhuận của công ty tăng dần khi số tiền chi cho quảng cáo tăng từ 0 đến 40 nghìn USD

Lợi nhuận của công ty giảm dần khi số tiền chi cho quảng cáo lớn hơn 40 nghìn USD và khi đó, càng tăng tiền quảng cáo thì lợi nhuận càng giảm.

Lời giải Sách bài tập Toán lớp 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác: