Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu

Giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

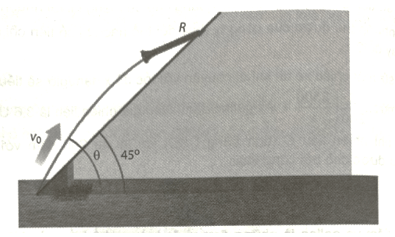
Bài 1.19 trang 16 SBT Toán 12 Tập 1: Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu v₀ (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc 45° so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet = 0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số

R(θ) = $\frac{v_{0}^{2} \sqrt{2}}{16} \cos θ (\sin θ - \cos θ) .$

Góc nén θ nào làm cho quãng đường R lớn nhất? Giá trị lớn nhất của R là bao nhiêu?

Lời giải:

Ta có: R(θ) = $\frac{v_{0}^{2} \sqrt{2}}{16} (\cos θ \sin θ - \cos^{2} θ)$ = $\frac{v_{0}^{2} \sqrt{2}}{32} (\sin 2 θ - \cos 2 θ - 1)$ , 45° ≤ θ ≤ 90°.

Do đó: R'(θ) = $\frac{v_{0}^{2} \sqrt{2}}{16} (\cos 2 θ + \sin 2 θ)$

R'(θ) = 0 ⇔ 2θ = 135° ⇔ θ = 67,5° (do 45° ≤ θ ≤ 90°).

Mặt khác, R(45°) = 0; R(67,5°) = $\frac{v^{2} (2 - \sqrt{2})}{32}$ ; R(90°) = 0.

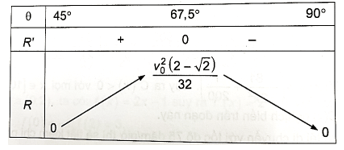
Ta có bảng biến thiên như sau:

Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu

Vậy khi góc ném θ = 67,5° thì quãng đường R là lớn nhất và bằng $\frac{v^{2} (2 - \sqrt{2})}{32}$ feet, trong đó v₀ (feet/giây) là vận tốc ban đầu của vật.

Lời giải Sách bài tập Toán lớp 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác:

SBT Toán 12 Kết nối

Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu

Giải sách bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Xem thêm các bài giải sách bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác: